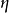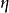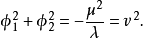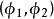如果某種連續整體對稱性是自發破缺的,則一定存在零質量的玻色子,即Goldstone玻色子。原來由復標量場描述的量子系統,當發生對稱性自發破缺後就轉化為實際量粒子和Goldstone玻色子構成的量子系統。
基本介紹
- 中文名:goldstone玻色子
- 外文名:Goldstone boson
- 定義:零質量的玻色子
- 套用學科:量子力學術語
- 範疇:數理科學
- 涉及:玻色子
概念,基本原理,
概念
如果某種連續整體對稱性是自發破缺的,則一定存在零質量的玻色子,即Goldstone玻色子。原來由復標量場描述的量子系統,當發生對稱性自發破缺後就轉化為實際量粒子和Goldstone玻色子構成的量子系統。當體系的連續對稱性自發破缺時,會產生一種無能隙的無自旋玻色子(spinless boson)。聲子就是一種goldstone玻色子,並且你會發現在其色散關係中,長波極限下能量為0。
基本原理
考慮經典復標量場的拉氏密度:

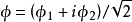
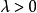
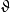
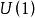
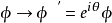
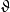
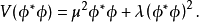
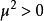
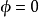
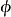
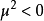
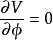

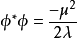
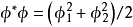
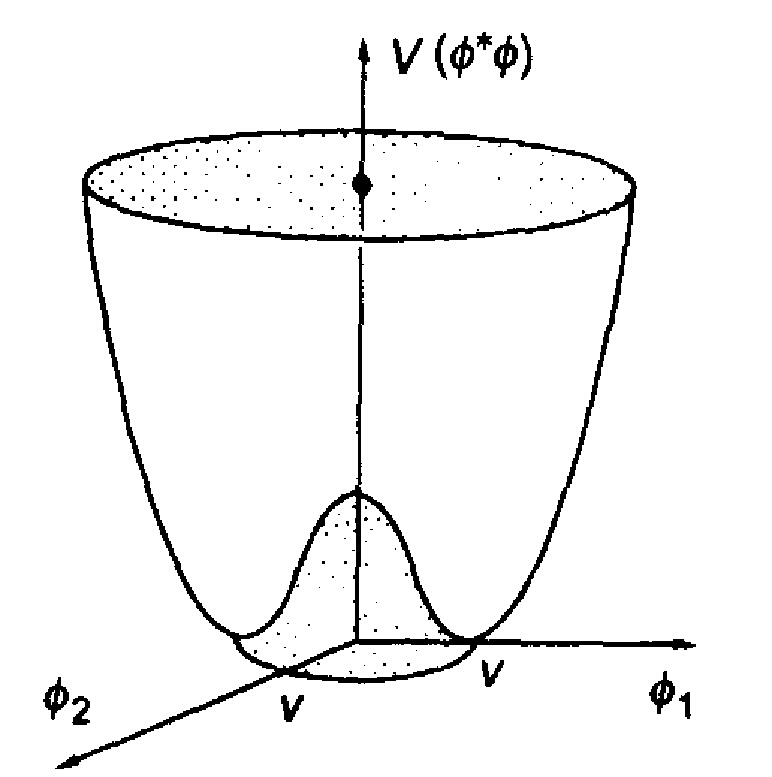 圖1
圖1各點之間的相互關係由相位變換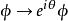 決定。像前例一樣,選定一個真空態:
決定。像前例一樣,選定一個真空態:
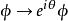
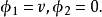

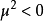
引入新的場量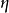 和
和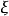 ,滿足
,滿足
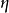
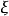
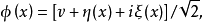
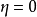
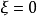
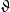
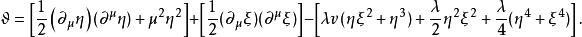
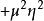
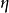
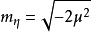
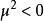
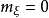
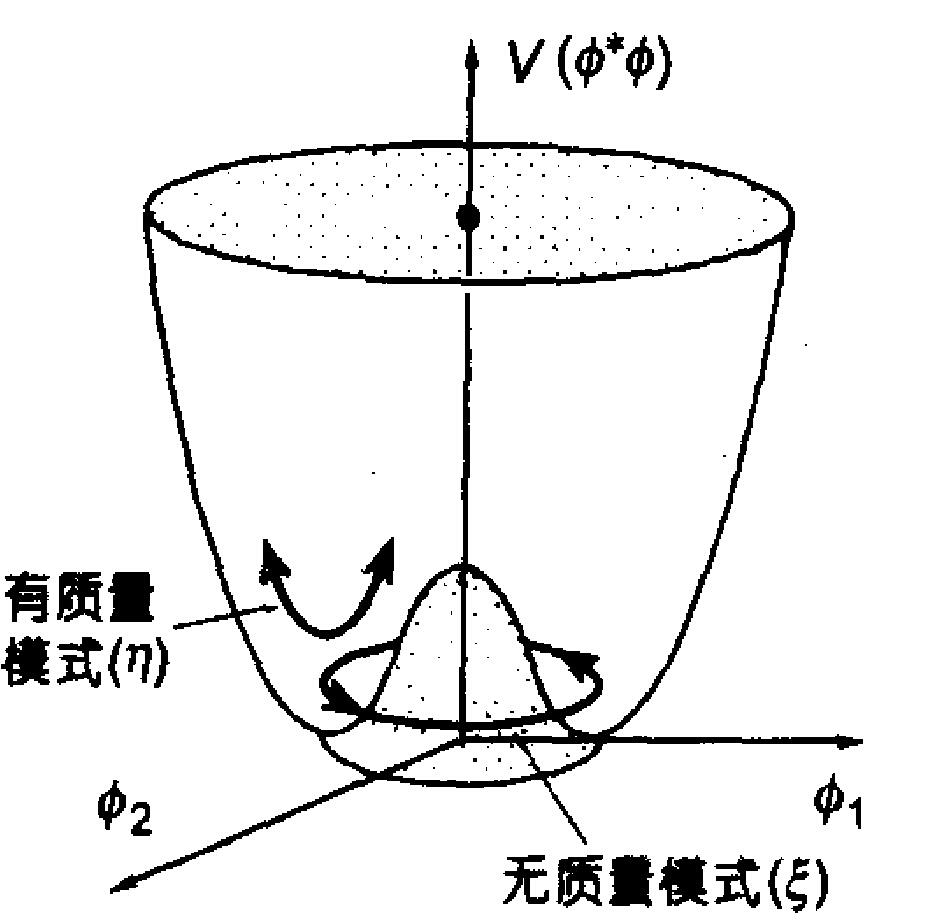 圖2
圖2勢能最小處位於谷底的圓周上。有質量的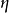 模式對應於有恢復力的“徑向振盪”,通常說,
模式對應於有恢復力的“徑向振盪”,通常說,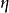 場自發地獲得了它的質量;無質量的
場自發地獲得了它的質量;無質量的 模式對應於谷底圓周上的無阻尼運動(無質量激發)。谷底圓周上的無數個點的整體具有嚴格的旋轉對稱性,但是現實的真空態只有一個,只能是其中一點.對於這一點(即現實的真空態)來說,原有的旋轉對稱性就不再保持了。這也就是對稱性的自發破缺。
模式對應於谷底圓周上的無阻尼運動(無質量激發)。谷底圓周上的無數個點的整體具有嚴格的旋轉對稱性,但是現實的真空態只有一個,只能是其中一點.對於這一點(即現實的真空態)來說,原有的旋轉對稱性就不再保持了。這也就是對稱性的自發破缺。