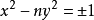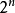X²+1素數

X為一整數，若K=X²+1是一素數，則稱K為X²+1素數。

其核心問題是X²+1素數猜想：是否存在無窮多個X²+1素數？

基本介紹

• 中文名：X2+1素數
• 外文名：X2+1 Primes
• 別名：X2+1質數
• 套用領域：數學
• 核心問題：X2+1素數猜想

2+1素數猜想" >x²+1素數猜想

人們很早就發現了許多正整數的平方加1以後是素數，例如：

1²+1=2，素數；2²+1=5，素數；4²+1=17，素數；6²+1=37，素數；10²+1=101，素數；

14²+1=197，素數；16²+1=257，素數； 20²+1=401，是素數；24²+1=577，是素數；……。

這種類型的素數有多少？是否有無窮個？

1900年，在法國巴黎召開了第二屆國際數學家大會，戴維·希爾伯特發表了《未來的數學問題》這個著名的講演， 在第25自然段談到這個問題，問是否有無窮個x²+1素數，正式將x²+1素數猜想提到了全球數學家的面前，成為與哥德巴赫猜想和孿生素數猜想同時代的著名數學難題。遺憾的是，到目前為止，尚未有人證明此猜想是成立的。

《10000個科學難題（數學卷）》（科學出版社，2009年5月第一版，第102頁）指出：是否有無窮個正整數x，使得x²+1總是素數？這個問題比孿生素數猜想更加困難，這是因為在正整數中，形如x²+1的數比p+2稀少，所以x²+1為素數的機率更小。

2+1素數與費馬數" >x²+1素數與費馬數

x²+1素數與費馬數相關。費馬數 可以表示為 的形式，即只要 為偶數即可。

如果x²+1素數有限，也即費馬素數有限，那么費馬合數就無窮。

2+1合數與佩爾方程" >X²+1合數與佩爾方程

由於問題的困難，人們開始關注X²+1合數，企圖從X²+1合數的蛛絲馬跡中尋找X²+1素數。發現許許多多X²+1合數有平方因子 例如：18²+1=325=5²×13；32²+1=1025=5²×41；38²+1=1445=5×17²；68²+1=4625=5³×37；70²+1=4901=13²×29；....。 這是一個佩爾方程形式：