u檢驗是一種用來評估兩個獨立的順序數據樣本是否來自同一個總體的非參數檢驗。使用u檢驗,首先需要將兩個獨立樣本的分數轉化為其所在合併樣本中的名次(順序數據),然後檢驗基於兩樣本名次計算出的u值,以此來評估兩組的平均名次間是否具有顯著差異。
基本介紹
- 中文名:u檢驗
- 外文名:u-test
- 類別:統計檢驗法
- 套用學科:統計學
- 前提:大樣本
- 套用領域:數理化學
定義
計算公式

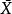
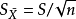
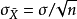

u檢驗與t檢驗
率的u檢驗

u檢驗是一種用來評估兩個獨立的順序數據樣本是否來自同一個總體的非參數檢驗。使用u檢驗,首先需要將兩個獨立樣本的分數轉化為其所在合併樣本中的名次(順序數據),然後檢驗基於兩樣本名次計算出的u值,以此來評估兩組的平均名次間是否具有顯著差異。

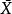
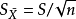
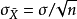


u檢驗是一種用來評估兩個獨立的順序數據樣本是否來自同一個總體的非參數檢驗。使用u檢驗,首先需要將兩個獨立樣本的分數轉化為其所在合併樣本中的名次(順序數據),...
u—檢驗法是在大樣本(n>30)的情況下,檢驗隨機變數的數學期望是否等於某一已知值的一種假設檢驗方法。設X1,X2,……,Xn是正態隨機變數X的一個樣本,總體方差為...
顯著性檢驗(significance test)就是事先對總體(隨機變數)的參數或總體分布形式做出一個假設,然後利用樣本信息來判斷這個假設(備擇假設)是否合理,即判斷總體的真實...
曼-惠特尼U檢驗又稱“曼-惠特尼秩和檢驗”,是由H.B.Mann和D.R.Whitney於1947年提出的。它假設兩個樣本分別來自除了總體均值以外完全相同的兩個總體,目的是檢驗...
非參數檢驗(Nonparametric tests)是統計分析方法的重要組成部分,它與參數檢驗共同構成統計推斷的基本內容。非參數檢驗是在總體方差未知或知道甚少的情況下,利用樣本數據...
應注意的是當n>25時,可用正態近似法計算u值進行u檢驗,當相同秩次較多時u值需進行校正。秩和檢驗成組 兩樣本成組資料的比較套用Wilcoxon秩和檢驗,其基本思想是:...
套用條件與t檢驗基本一致,只是當大樣本時用U檢驗,而小樣本時則用t檢驗,t檢驗可以代替U檢驗。差異顯著性檢驗方差分析 用於常態分配、方差齊性的多組比較,即多個...
單邊檢驗(one-sided test)亦稱單尾檢驗,又稱單側檢驗.在假設檢驗中,用檢驗統計量的密度曲線和二軸所圍成面積中的單側尾部面積來構造臨界區域進行檢驗的方法稱為...
雙邊檢驗(two-sided test),亦稱雙尾檢驗、雙側檢驗.在假設檢驗中,用檢驗統計量的密度曲線和x軸所圍成的面積的左右兩邊的尾部面積來構造臨界區域進行檢驗的方法。....
(五)多樣本非參數檢驗 [1] Kruskal-Wallis檢驗實質是兩獨立樣本的曼-惠特尼U檢驗在多個樣本下的推廣。(秩和檢驗).Jonckheere-Terpstra檢驗有點像KW檢驗後進一步...
