S1指標是在圓周群S1作用下的指標,最早是由拉比諾維茨等人引進的。
基本介紹
- 中文名:S1指標
- 外文名:S1-index
- 適用範圍:數理科學
簡介,指標理論,
簡介
S1指標是在圓周群S1作用下的指標。S1指標最早是由拉比諾維茨等人引進的。
設S1=R/[0,2π],X為T(S1)空間,Z={A⊂X|A是T(S1)不變閉子集}。定義γ:∑→∑+∪{+∞}如下:
當A=∅時,令γ(∅)=0。
當A∈∑,A≠0時,令Y(A)=min{n∈Z+|存在k∈Z+與連續映射φ:A→Cn\{0},使得φ(Tθx)=eikθφ(x),∀x∈ A,∀θ∈S1},其中Cn為復n維線性空間。若所述之n不存在,則令γ(A)=+∞。
如此定義的γ就是X上的S1指標。
指標理論
指標理論是疇數理論在T(G)不變泛函情形的變種形式。
設G是緊拓撲群,X是T(G)空間,∑={A⊂X|A是T(G)不變閉集}。若函式i:∑→Z+∪{+∞}滿足下述條件:
1、平凡性。i(A)=0⇔A=∅。
2、單調性。A,B∈∑,A⊂B⇒i(A)≤i(B)。
3、次可加性。∀A,B∈∑,i(A∪B)≤i(A)+i(B)。
4、超變性。若A∈∑,h=η(∙,1),η:[0,1]×X→X是T(G)等變形變,則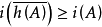 。
。
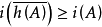
5、連續性。若A∈∑,A緊,則存在A的某個閉鄰域N∈∑,使得i(N)=i(A),則稱i為X上的一個T(G)指標。
