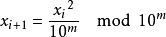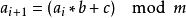隨機數生成器（Random Numeral Generator，即RNG）是用於生成隨機數的程式或硬體。
基本介紹
- 中文名：隨機數生成器
- 外文名：Random Numeral Generator
真隨機數生成器,偽隨機數生成器,平方取中法,線性同餘法,
真隨機數生成器
真隨機數生成器的生成方法有很多種。
PuTTYgen的隨機數是讓用戶移動滑鼠達到一定的長度，之後把滑鼠的運動軌跡轉化為種子；Intel通過電阻和振盪器來生成熱噪聲作為信息熵資源；Unix/Linux的dev/random和/dev/urandom採用硬體噪音生成隨機數。
在Intel 815E晶片組的個人電腦上安裝Intel Security Driver(ISD)後,可以通過編程讀取暫存器獲取RNG中的隨機數。
此外還有提供真隨機數的網站，如：
- Quantum Random Bit Generator Service (QRBGS)是一個免費為學術和科研機構提供真隨機數字服務的網站，由克羅地亞的計算機科學家開發。其隨機性依賴於半導體光子發散量子物理過程中內在的隨機性，光子通過光電效應進行檢測。這些隨機檢測到的光子都是相互獨立的。它可以通過C/C++庫、Web Service、Mathmatic/Matlab外掛程式等多種方式訪問。
- Randomness and Integrity Services Ltd. ，從1998年開始在Internet上提供真隨機數服務，它用大氣噪音生成真隨機數。
偽隨機數生成器
生成偽隨機數有很多種算法，其中常用的有平方取中法、線性同餘法、馬特賽特旋轉演算法等。
平方取中法
平方取中法是由馮·諾依曼在1946年提出的，其基本思想為：將數列中的第a(i)項（假設其有m位）平方，取得到的2m位數（若不足2m位，在最高位前補0）中間部分的m位數字，作為a(i)的下一項a(i+1)，由此產生一個偽隨機數數列。即：
（其中m為
的位數）
平方取中法計算較快，但在實際套用時會發現該方法容易產生周期性明顯的數列，而且在某些情況下計算到一定步驟後始終產生相同的數甚至是零，或者產生的數字位數越來越小直至始終產生零。所以用平方取中法產生偽隨機數數列時不能單純使用公式，應該在計算過程中認為加入更多變化因素，比如根據前一個數的奇偶性進行不同的運算，如果產生的數字位數減少時通過另一種運算使其恢復成m位。
線性同餘法
線性同餘方法是目前套用廣泛的偽隨機數生成算法，其基本思想是通過對前一個數進行線性運算並取模從而得到下一個數。即：
其中b稱為乘數，c稱為增量，m稱為模數，它們均為常數。
乘數、增量和模數的選取可以多種多樣，只要保證產生的隨機數有較好的均勻性和隨機性即可。
線性同餘法的最大周期是m，但一般情況下會小於m。要使周期達到最大，應該滿足以下條件：
(1)c和m互質；
(2)m的所有質因子的積能整除b-1；
(3)若m是4的倍數，則b-1也是；
(4)b，c，a(0)（初值，一般即種子）都比m小；
(5)b，c是正整數。
