基本介紹
- 外文名:R-tree
- 性質:向多維空間發展的另一種形式
- 空間對象:按範圍劃分
- 解釋:R-Tree是n 叉樹
基本簡介,數據結構,性質簡介,算法描述,其他索引結構,R+樹,R*樹,QR樹,SS樹,X樹,
基本簡介
R-tree是B-tree向多維空間發展的另一種形式,它將空間對象按範圍劃分,每個結點都對應一個區域和一個磁碟頁,非葉結點的磁碟頁中存儲其所有子結點的區域範圍,非葉結點的 所有子結點的區域都落在它的區域範圍之內;葉結點的磁碟頁中存儲其區域範圍之內的所有空間對象的外接矩形。每個結點所能擁有的子結點數目有上、下限,下限 保證對磁碟空間的有效利用,上限保證每個結點對應一個磁碟頁,當插入新的結點導致某結點要求的空間大於一個磁碟頁時,該結點一分為二(分裂)。R樹是一種動態索引結構,即:它的查詢可與插入或刪除同時進行,而且不需要定期地對樹結構進行重新組織。
數據結構
R-Tree是一種空間索引數據結構,下面做簡要介紹:
(1)R-Tree是n 叉樹,n稱為R-Tree的扇(fan)。
(2)每個結點對應一個矩形。
(3)葉子結點上包含了小於等於n 的對象,其對應的矩為所有對象的外包矩形。
(4)非葉結點的矩形為所有子結點矩形的外包矩形。
R-Tree的定義很寬泛,同一套數據構造R-Tree,不同方可以得到差別很大的結構。什麼樣的結構比較優呢?有兩標準:
(1)位置上相鄰的結點儘量在樹中聚集為一個父結點。
(2)同一層中各兄弟結點相交部分比例儘量小。
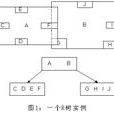
R-樹是一種用於處理多維數據的數據結構,用來訪問二維或者更高維區域對象組成的空間數據.R樹是一棵平衡樹。樹上有兩類結點:葉子結點和非葉子結點。每一個結點由若干個索引項構成。對於葉子結點,索引項形如(Index,Obj_ID)。其中,Index表示包圍空間數據對象的最小外接矩形MBR,Obj_ID標識一個空間數據對象。對於一個非葉子結點,它的索引項形如(Index,Child_Pointer)。 Child_Pointer 指向該結點的子結點。Index仍指一個矩形區域,該矩形區域包圍了子結點上所有索引項MBR的最小矩形區域。一棵R樹的示例如圖所示: r-tree圖
r-tree圖
 r-tree圖
r-tree圖性質簡介
符號說明:M:結點中單元的最大數目,m(1<= m <= M/2)為非根結點中單元個數的下限。
一個R樹滿足如下性質:
(1) 每一個葉子結點中包含的單元的個數介於m和M之間,除非他同樣是根結點
(2) 每一個葉子結點中的單元(I, tuple-identifier),I為包含所有子結點的最小包含矩形(MBR),tuple-identifier是指向存儲記錄的指針。
(3) 每一個非葉子結點的子結點數介於m和M之間,除非他是根結點
(4) 每一個非葉子結點單元(I, child -pointer)I是包含子結點的最小矩形MBR,child-pointer是指向子結點的指針。通過該指針逐層遞歸,可以訪問到葉子結點。
(5) 根結點至少有兩個子結點,除非他同時是葉子結點
(6) 所有的葉子結點都處在樹的同一層上。
算法描述
算法描述如下:
對象數為n,扇區大小定為fan。
(1)估計葉結點數k=n/fan。
(2)將所有幾何對象按照其矩形外框中心點的x值排序。
(3)將排序後的對象分組,每組大小為 *fan,最後一組可能不滿員。
(4)上述每一分組內按照幾何對象矩形外框中心點的y值排序。
(5)排序後每一分組內再分組,每組大小為fan。
(6)每一小組成為葉結點,葉子結點數為nn。
(7)k=nn,返回1。
其他索引結構
R+樹
在Guttman的工作的基礎上,許多R樹的變種被開發出來, Sellis等提出了R+樹,R+樹與R樹類似,主要區別在於R+樹中兄弟結點對應的空間區域無重疊,這樣劃分空間消除了R樹因允許結點間的重疊而產生的“死區域”(一個結點內不含本結點數據的空白區域),減少了無效查詢數,從而大大提高空間索引的效率,但對於插入、刪除空間對象的操作,則由於操作要保證空間區域無重疊而效率降低。同時R+樹對跨區域的空間物體的數據的存儲是有冗餘的,而且隨著資料庫中數據的增多,冗餘信息會不斷增長。Greene也提出了他的R樹的變種。
R*樹
在1990年,Beckman和Kriegel提出了最佳動態R樹的變種——R*樹。R樹和R樹一樣允許矩形的重疊,但在構造算法R*樹不僅考慮了索引空間的“面積”,而且還考慮了索引空間的重疊。該方法對結點的插入、分裂算法進行了改進,並採用“強制重新插入”的方法使樹的結構得到最佳化。但R*樹算法仍然不能有效地降低空間的重疊程度,尤其是在數據量較大、空間維數增加時表現的更為明顯。R*樹無法處理維數高於20的情況。
QR樹
QR樹利用四叉樹將空間劃分成一些子空間,在各子空間內使用許多R樹索引,從而改良索引空間的重疊。QR樹結合了四叉樹與R樹的優勢,是二者的綜合套用。實驗證明:與R樹相比,QR樹以略大(有時甚至略小)的空間開銷代價,換取了更高的性能,且索引目標數越多,QR樹的整體性能越好。
SS樹
SS樹對R樹進行了改進,通過以下措施提高了最鄰近查詢的性能:用最小邊界圓代替最小邊界矩形表示區域的形狀,增強了最鄰近查詢的性能,減少將近一半存儲空間;SS樹改進了R樹的強制重插機制。當維數增加到5是,R樹及其變種中的邊界矩形的重疊將達到90%,因此在高維情況(≧5)下,其性能將變的很差,甚至不如順序掃描。
X樹
X樹是線性數組和層狀的R樹的雜合體,通過引入超級結點,大大地減少了最小邊界矩形之間的重疊,提高了查詢效率。X樹用邊界圓進行索引,邊界矩形的直徑(對角線)比邊界圓大,SS樹將點分到小直徑區域。由於區域的直徑對最鄰近查詢性能的影響較大,因此SS樹的最鄰近查詢性能優於R樹;邊界矩形的平均容積比邊界圓小,R樹將點分到小容積區域;由於大的容積會產生較多的覆蓋,因此邊界矩形在容積方面要優於邊界圓。SR樹既採用了最小邊界圓(MBS),也採用了最小邊界矩形(MBR),相對於SS樹,減小了區域的面積,提高了區域之間的分離性,相對於R樹,提高了鄰近查詢的性能。