NP-hard，其中，NP是指非確定性多項式（non-deterministic polynomial，縮寫NP）。所謂的非確定性是指，可用一定數量的運算去解決多項式時間內可解決的問題。
NP問題通俗來說是其解的正確性能夠被“很容易檢查”的問題，這裡“很容易檢查”指的是存在一個多項式檢查算法。若NP中所有問題到某一個問題是圖靈可歸約的，則該問題為NP-hard問題。
基本介紹
- 外文名：NP-hard
- 全稱：non-deterministic polynomial
- 釋義：所謂的非確定性
- 作用：解決問題
NP-hard,形式化定義,
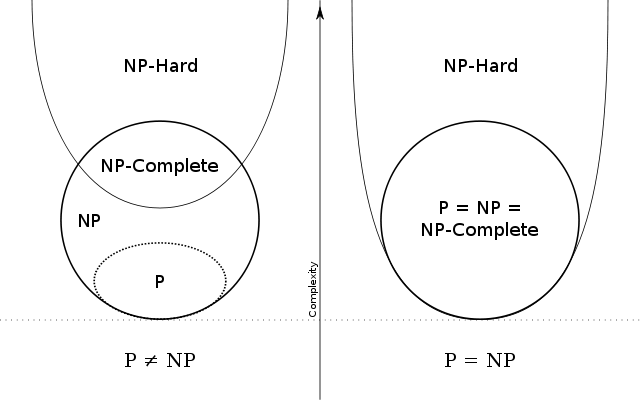
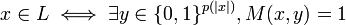NP-hard
其中，NP是指非確定性多項式（non-deterministic polynomial，縮寫NP）。所謂的非確定性是指，可用一定數量的運算去解決多項式時間內可解決的問題。
例如，著名的推銷員旅行問題（Travel Saleman Problem or TSP）：假設一個推銷員需要從香港出發，經過廣州，北京，上海，…，等 n 個城市， 最後返回香港。 任意兩個城市之間都有飛機直達，但票價不等。假設公司只給報銷 C 元錢，問是否存在一個行程安排，使得他能遍歷所有城市，而且總的路費小於 C？
推銷員旅行問題顯然是 NP 的。因為如果你任意給出一個行程安排，可以很容易算出旅行總開銷。但是，要想知道一條總路費小於 C 的行程是否存在，在最壞情況下，必須檢查所有可能的旅行安排！ 這將是個天文數字。
旅行推銷員問題是數圖論中最著名的問題之一，即“已給一個n個點的完全圖，每條邊都有一個長度，求總長度最短的經過每個頂點正好一次的封閉迴路”。Edmonds，Cook和Karp等人發現，這批難題有一個值得注意的性質，對其中一個問題存在有效算法時，每個問題都會有有效算法。
迄今為止，這類問題中沒有一個找到有效算法。傾向於接受NP完全問題（NP-Complete或NPC）和NP難題（NP-Hard或NPH）不存在有效算法這一猜想，認為這類問題的大型實例不能用精確算法求解，必須尋求這類問題的有效的近似算法。
此類問題中，經典的還有 子集和問題； Hamilton迴路問題；最大團問題
形式化定義
常用的定義是所謂的“關係定義式”。即對於一個語言L，L在NP中，那么存在多項式時間圖靈機M，和多項式p使得
