基本介紹
- 中文名:馬拉車算法
- 外文名:Manachar algorithm
- 例題:拉拉隊排練 最長雙回文串
- 領域:計算機科學
- 套用:求回文串
- 時間複雜度:O(N)
基本介紹,Manacher算法原理與實現,(1)Len數組簡介與性質,(2)Len數組的計算,時間複雜度分析,例題,問題描述,Input,Output,Sample Input,Sample Output,C++代碼:,
基本介紹
Manachar算法主要是處理字元串中關於回文串的問題的,它可以在 O(n) 的時間處理出以字元串中每一個字元為中心的回文串半徑,由於將原字元串處理成兩倍長度的新串,在每兩個字元之間加入一個特定的特殊字元,因此原本長度為偶數的回文串就成了以中間特殊字元為中心的奇數長度的回文串了。
Manacher算法原理與實現
Manacher算法提供了一種巧妙的辦法,將長度為奇數的回文串和長度為偶數的回文串一起考慮,具體做法是,在原字元串的每個相鄰兩個字元中間插入一個分隔設定,同時在首尾也要添加一個分隔設定,分隔設定的要求是不在原串中出現,一般情況下可以用#號。
(1)Len數組簡介與性質
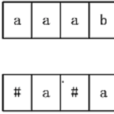
Manacher算法用一個輔助數組Len[i]表示以字元T[i]為中心的最長回文字串的最右字元到T[i]的長度,比如以T[i]為中心的最長回文字串是T[l,r],那么Len[i]=r-i+1。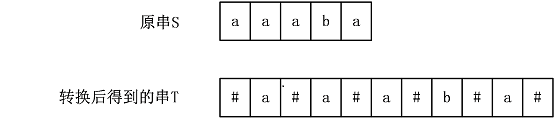

對於右圖,可以得出Len[i]數組為:

Len 數組有一個性質,那就是Len[i]-1就是該回文子串在原字元串S中的長度。
證明:
首先在轉換得到的字元串T中,所有的回文字串的長度都為奇數,那 么對於以T[i]為中心的最長回文字串,其長度就為2*Len[i]-1,經過觀察可知,T中所有的回文子串,其中分隔設定的數量一定比其他字元的數量多 1,也就是有Len[i]個分隔設定,剩下Len[i]-1個字元來自原字元串,所以該回文串在原字元串中的長度就為Len[i]-1。
(2)Len數組的計算
首先從左往右依次計算Len[i],當計算Len[i]時,Len[j](0<=j<i)已經計算完畢。設P為之前計算中最長回文子串的右端點的最大值,並且設取得這個最大值的位置為po,分兩種情況:
第一種情況:i<=P
那么找到i相對於po的對稱位置,設為j,那么如果Len[j]<P-i,如下圖:

那么說明以j為中心的回文串一定在以po為中心的回文串的內部,且j和i關於位置po對稱,由回文串的定義可知,一個回文串反過來還是一個回文串,所以以i 為中心的回文串的長度至少和以j為中心的回文串一樣,即Len[i]>=Len[j]。因為Len[j]<P-i,所以說i+Len[j]& lt;P。由對稱性可知Len[i]=Len[j]。
如果Len[j]>=P-i,由對稱性,說明以i為中心的回文串可能會延伸到P之外,而大於P的部分我們還沒有進行匹配,所以要從P+1位置開始一個一個進行匹配,直到發生失配,從而更新P和對應的po以及Len[i]。
第二種情況:i>P
如果i比P還要大,說明對於中點為i的回文串還一點都沒有匹配,這個時候,就只能老老實實地一個一個匹配了,匹配完成後要更新P的位置和對應的po以及Len[i]。

時間複雜度分析
Manacher 算法的時間複雜度分析和Z算法類似,因為算法只有遇到還沒有匹配的位置時才進行匹配,已經匹配過的位置不再進行匹配,所以對於T字元串中的每一個位置,只 進行一次匹配,所以Manacher算法的總體時間複雜度為O(n),其中n為T字元串的長度,由於T的長度事實上是S的兩倍,所以時間複雜度依然是線性的。
例題
問題描述
據說如果你給無限只母牛和無限台巨型攜帶型電腦(有非常大的鍵盤),那么母牛們會製造出世上最棒的回文。你的工作就是去尋找這些牛製造的奇觀(最棒的回文)。
在尋找回文時不用理睬那些標點符號、空格(但應該保留下來以便做為答案輸出),只用考慮字母'A'-'Z'和'a'-'z'。要你尋找的最長的回文的文章是一個不超過20,000個字元的字元串。我們將保證最長的回文不會超過2,000個字元(在除去標點符號、空格之前)。
在尋找回文時不用理睬那些標點符號、空格(但應該保留下來以便做為答案輸出),只用考慮字母'A'-'Z'和'a'-'z'。要你尋找的最長的回文的文章是一個不超過20,000個字元的字元串。我們將保證最長的回文不會超過2,000個字元(在除去標點符號、空格之前)。
Input
輸入檔案不會超過20,000字元。這個檔案可能一行或多行,但是每行都不超過80個字元(不包括最後的換行符)。
Output
輸出的第一行應該包括找到的最長的回文的長度。
下一行或幾行應該包括這個回文的原文(沒有除去標點符號、空格),把這個回文輸出到一行或多行(如果回文中包括換行符)。
如果有多個回文長度都等於最大值,輸出最前面出現的那一個。
下一行或幾行應該包括這個回文的原文(沒有除去標點符號、空格),把這個回文輸出到一行或多行(如果回文中包括換行符)。
如果有多個回文長度都等於最大值,輸出最前面出現的那一個。
Sample Input
Confucius say: Madam, I'm Adam.
Sample Output
11
Madam, I'm Adam
Madam, I'm Adam
C++代碼:
#include<iostream>#include<stdlib.h>#include<stdio.h>#include<string.h>#include<string>#include<cmath>using namespace std;char s[50001];char ss[50001];int p[50001];int lenss,lens,id=0,maxlen=0,maxn,cnt;int main(){ int i=0; while(scanf("%c",&s[i])!=EOF) { if(s[i]<=90&&s[i]>=65) ss[lenss++]=char(s[i]); else if(s[i]<=122&&s[i]>=97) ss[lenss++]=char(s[i]-32); i++; } for(int i=lenss; i>=0; --i) //插入'#' { ss[i+i+2]=ss[i]; ss[i+i+1]='#'; }//插入了len+1個'#',最終的s長度是1~len+len+1即2*len+1,首尾s[0]和s[2*len+2]要插入不同的字元 ss[0]='*';//s[0]='*',s[len+len+2]='\0',防止在while時p[i]越界 for(int i=2; i<2*lenss+1; ++i) { if(p[id]+id>i)p[i]=min(p[2*id-i],p[id]+id-i); else p[i]=1; while(ss[i-p[i]] == ss[i+p[i]])++p[i]; if(id+p[id]<i+p[i])id=i; if(maxlen<p[i]) { maxlen=p[i]; maxn=i; } } cout<<maxlen-1<<endl; int x; if(maxn%2==0) x=maxn/2; else x=(maxn+1)/2; int lens=strlen(s); cnt=0; for(i=0; i<=lens-1; i++) { if((65<=s[i]&&s[i]<=90)||(97<=s[i]&&s[i]<=122)) cnt++; if(cnt>=x-(maxlen-1)/2) printf("%c",s[i]); if(cnt==x-(maxlen-1)/2+maxlen-2) break; } cout<<endl; return 0;}