M/G/1模型(M/G/1 model)是一種排隊模型,指服務時間T的分布是一般的,但要求期望值E[T]和方差var[T]都存在,其他條件和標準的M/M/1模型相同的排隊模型。
其運行指標為
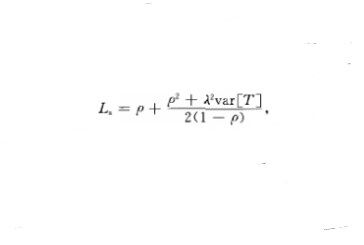
式中p=}E[T]G1,稱上式為P-K公式.只要知道}l , E [T]和var[T],無論T是什麼分布,都可以求出Ls.然後,通過Wz=Wq+E[T],Lz一}1Ws和L4 =幾W。可以求1 q,W。和WS.值得注意的是,要想改進上述各指標,因僅當var [T】一。時,隨機性的波動才不影響Ls,故除考慮期望值外,還可以用改變方差來考慮.對M/G/ 1 /二系統,肯德爾(Kendall , D.U.)首先使用了嵌入馬氏鏈的分析方法.雖然該系統的隊長過程{N(t),t}0}不具有馬氏性,但在{N(t>,t}0}中可嵌入一個離散參數的馬氏鏈.利用馬氏鏈的理論得到嵌入馬氏鏈的極限機率分布,該分布就是原過程{N<t>,t>o}當t~二時的平穩分布,顧客離去時刻是該過程的再生點.時齊的、非周期的可列狀態馬氏鏈{N
,n,l},其一步轉移機率矩陣為

馬氏鏈{N
,n}l }是遍歷的充分必要條件為}/} _pGl.當pGl時,
且{二,}為惟一的平穩分布;當p)l時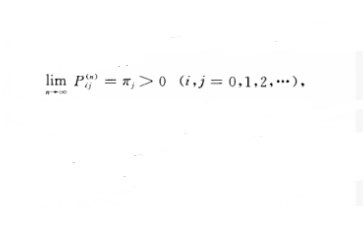
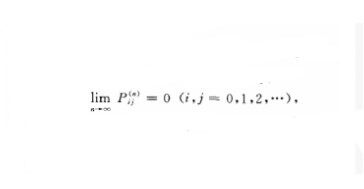
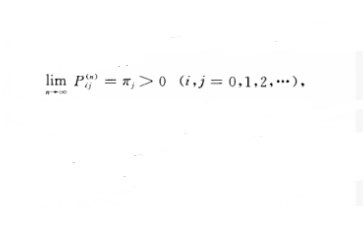
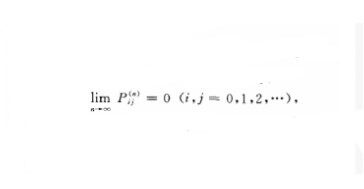
且不存在平穩分布,其中(屍忿”)為嵌入馬氏鏈的n步轉移矩陣.對任何正整數m,有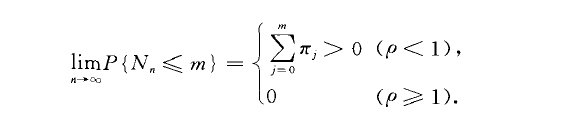
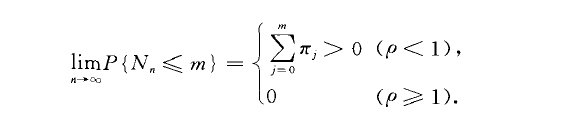
當p妻1時,不論怎樣大的m,當n~二時,第n個顧客服務結束,離開時系統中留下的隊長毛、的機率總趨於。.這說明隊將愈來愈長,系統達不到統計平衡,即系統是不穩定的.若p=1,則{N
,n}l}為零常返鏈;若p>1,則{N},n>1}為非常返鏈.對這兩種情形均不存在平穩分布.當p=1時,服務機構始終不空的機率為0;而當p>1時,服務機構始終不空的機率為正.當pGl時,
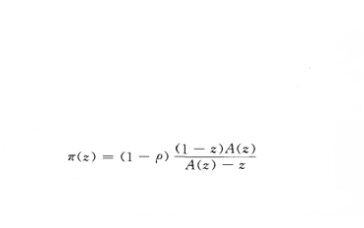
是馬氏鏈{N
,n,l}平穩狀態分布{n}}的母函式的表達式.二。=P
,n,0,二,就是在統計平衡下,任一時刻系統有n個顧客的機率.
