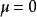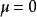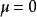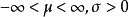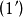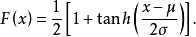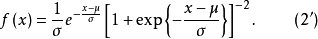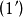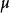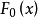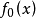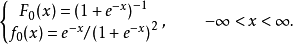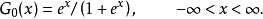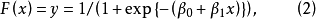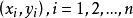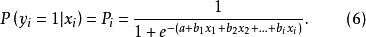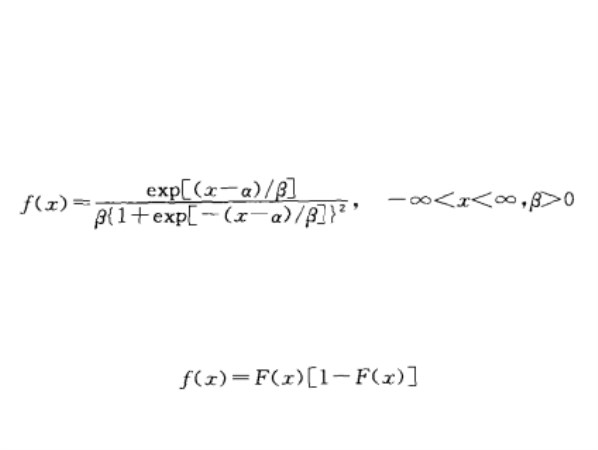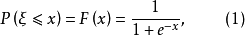基本介紹
定義一
則稱
服從
logistic分布,這個分布函式叫做
logistic函式,其圖形見圖1,此曲線叫做
logistic曲線。其密度函式為
 圖1a logistic分布函式
圖1a logistic分布函式 圖1b logistic密度函式
圖1b logistic密度函式由圖可見
的期望值
,密度函式對
對稱。分布函式F(x)在
處等於005。(0,0,5)為曲線F(x)的對稱點,而F(x)=0及F(x)=1為其漸近線。在(0,0,5)點處F(x)的斜率m=0.25。這是logistic函式的最簡單的形式。
定義二
Logistic分布函式為
式還告訴我們,Logistic分布仍然是屬於位置-尺度參數族,其中
是位置參數。
是尺度參數,這樣凡與位置-尺度參數族有關的結果,均對Logistic分布有效。當
時,相應的分布稱為標準Logistic分布,它的分布函式
與分布密度
為
因此有時上也從
出發,以它作為標準分布,經隨機變數線性變換後導出的分布作為一般的Logistic分布。
一元logistic函式
一般地,一元logistic函式可表為
式中
為二常值參數,隨
取值不同,分布的期望值
,以及對稱點,及對稱點處的斜率取值也不同,從而可形成一些不同的S形曲線;因此可依式(2)擬合某些S形曲線。不過此式中y的值域總是區間(0,1),且以y=0及y=1為其漸近線。
多元logistic函式
更一般的logistic函式為多元的(設為m元)
其中
皆為m+1維向量,
為參數向量,
,
到
則分別為變數
所可取的值,這些變數可以是連續的也可以是離散的。這個函式在不同條件下,或經不同的變換,可套用於不同的統計分析問題。
在研究來自同一總體的兩個變數(設為X和Y)間的關係時,採得容量為n的樣本
。畫出這組數據的散點圖,如曲線接近S形,可試用logistic曲線去擬合它。
Logistic回歸模型
模型概念
Logistic回歸模型是分析二分類型變數時常用的非線性統計模型,是最重要且套用最廣泛的非線性模型之一。該模型的因變數為二分類變數(y=0或y=1),結果變數與自變數間是非線性關係。形式如方程(1):
模型優缺點
優點:
第一,對變數要求低,可以接受非常態分配的數據;
第二,總體預測準確率較高;
第三,數據來源直接,操作簡便;
第四,判斷標準明確;
第五,模型穩定,利於推廣創新。
缺點:
第一,大多數時候對ST企業預測準確率較低;
第二,P值臨界點的選擇影響模型預測結果;
第三,違約樣本與正常樣本的比例影響預測結果。
模型原理
模型構造的原理簡單來說是運用對數運算將事件發生與否(即事件發生機率
或1)與自變數x間的非線性關係轉化為線性關係。以單一自變數為例,具體轉化步驟如下:
第一步,將上述Logistic模型方程(1)轉化為如下一個非線性方程(2)。
第二步,方程(2)化簡轉化為如下方程(3)。
第三步,方程(3)等式兩邊同時取對數轉化為如下方程(4)。
此時,
與
雖然不存線上性關係,但是關於P的函式記作logistic(P
i)與
存線上性關係。同理,自變數可拓展為m個,則有如下模型方程(5)。
以上得到的模型同樣可以用來預測事件的發生。預測時根據已知自變數與模型方程得出
,可以進一步計算事件發生的機率P。P處於0與1之間,越接近1表示發生的機率越大。
模型基本假設
第一,數據必須來自隨機樣本;
第四,自變數不需要呈常態分配。
模型套用步驟
第一步,選取樣本、確定初始指標;
第二步,篩選指標;
運用SPSS軟體對所有指標進行Kolmogorov-Smirnov常態分配檢驗。符合常態分配的指標進行顯著性T檢驗,不符合常態分配的數據進行Mann-Whitney顯著性檢驗,去除不顯著指標。進行Pearson檢驗,去除與其他指標存在高度相關性的指標。進行多重共線性檢驗,去除與其他指標存在多重共線性的指標;
第三步,進行KMO檢驗,確定是否進行因子分析;
第四步,進行Logistic回歸,得到模型,觀察模型擬合程度及預測準確率;
第五步,用檢驗樣本檢驗模型預測能力;
第六步,利用模型預測事件的發生機率。
模型參數解釋
因此,模型參量係數可以反映自變數x與事件發生機率P的關係。係數為正表明自變數x的增長促進事件的發生,係數為負表明自變數x的增長抑制事件的發生。

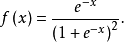
 圖1a logistic分布函式
圖1a logistic分布函式 圖1b logistic密度函式
圖1b logistic密度函式