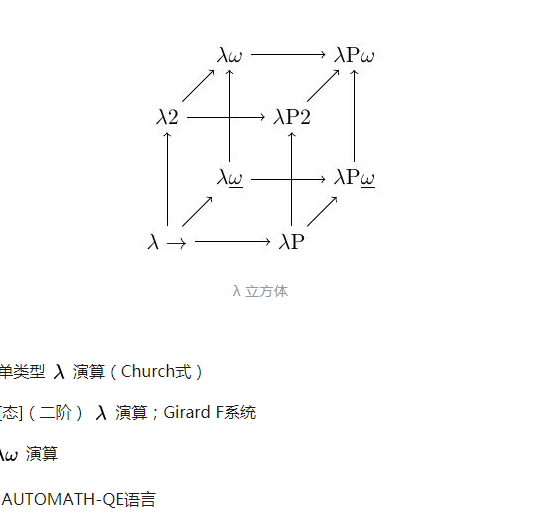
基本介紹
- 中文名:Lambda立方體
- 外文名:Lambda Cube
- 領域:類型輪
- 定義:探索構造演算中細化軸
- 抽象形式:值依賴類型、類型依賴類型
- 有關術語:簡單類型 λ-演算
構造演算,Lambda立方體抽象形式,λ-演算,依賴類型,
構造演算
構造演算(CoC)是高階有類型 lambda 演算,這裡的類型是一級值。因此在 CoC 內有可能定義從整數到類型、從類型到類型的函式,同從整數到整數的函式一樣。CoC 是強規範化的。CoC 最初由 Thierry Coquand 開發。CoC 是 Coq 定理證明器早期版本的基礎;它後來的版本建造在歸納構造演算之上,這是帶有對歸納數據類型的天然支持的 CoC 擴展。在最初的 CoC 中,歸納數據類型必須模擬為它們的多態解構函式。構造演算可以被當作 Curry-Howard同構的擴展。Curry-Howard 同構把在簡單類型 lambda 演算中項關聯上在直覺命題邏輯中自然演繹證明。構造演算擴展了這個同構為在完全的直覺謂詞邏輯中的證明,這包括了量化陳述(它也叫做"命題")的證明。
Lambda立方體抽象形式
Lambda立方體的每個軸都表示一種抽象形式:
- 值依賴類型,或多態。系統F,即二階λ-演算(圖中寫作 λ2)就是通過只加入此性質得到的。
- 類型依賴類型,或類型構造器。帶類型構造器的簡單類型 λ-演算(圖中為λω)就是通過只加入此性質得到的。它與系統F結合就產生了系統Fω(在圖中寫作不帶下劃線的λω)。
- 類型依賴值,或依賴類型。只加入此性質就得到了λΠ(在圖中寫作λP),一種與LF緊密相關的類型系統。
所有的八種演算包含了最基本的抽象形式,值依賴值即簡單類型 λ-演算中的普通函式。此立方中最豐富的演算即構造演算,它帶有所有三種抽象。所有八種演算都是強規範化的。然而子類型並未展示在此立方中,儘管像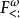 這樣以高階有界量化聞名的,結合了子類型和多態的系統具有實際意義,它可被進一步推廣為有界類型構造器。進一步擴展到
這樣以高階有界量化聞名的,結合了子類型和多態的系統具有實際意義,它可被進一步推廣為有界類型構造器。進一步擴展到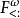 允許純函式對象的定義;這些系統通常在λ-立方的論文發表後才被卡發出來:
允許純函式對象的定義;這些系統通常在λ-立方的論文發表後才被卡發出來: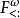 。此立方的思想來源於Henk Barendregt (1991)。就此立方的所有角而言,純類型系統的框架涵蓋了λ-立方,其它一些系統也可表示為此通用框架的實例。此框架的出現比λ-立方早上幾年。在 Barendregt 1991年的論文中,他也在此框架中定義了λ-立方的角。
。此立方的思想來源於Henk Barendregt (1991)。就此立方的所有角而言,純類型系統的框架涵蓋了λ-立方,其它一些系統也可表示為此通用框架的實例。此框架的出現比λ-立方早上幾年。在 Barendregt 1991年的論文中,他也在此框架中定義了λ-立方的角。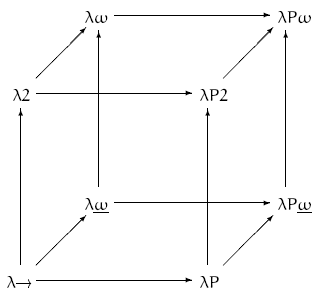 Lambda立方體
Lambda立方體
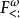
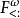
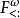
 Lambda立方體
Lambda立方體λ-演算
λ-演算(組合邏輯)及函式式語言及程式設計。大多數構造類型論都是用函式式語言實現的,而λ-演算是函式式語言的理論基礎,是函式式程式設計語言的純理論部分的範式,是由函式抽象和函式套用組成的系統,而這兩個特點也是程式設計語言所具有的共同之處:抽象與過程定義機制對應,套用與過程調用對應。
有類型 lambda 演算是使用 lambda 符號(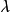 )指示匿名函式抽象的一種有類型的形式化。有類型 lambda 演算是基礎程式語言並且是有類型的函式式程式語言如 ML 和 Haskell 和更間接的指令式程式語言的基礎。它們通過 Curry-Howard同構密切關聯於直覺邏輯並可以被認為是範疇的類的內部語言,比如簡單類型 lambda 演算是笛卡爾閉範疇(CCC)的語言。有類型 lambda 演算被看作無類型lambda演算的精細化。更現代的觀點把有類型 lambda 演算看做更基礎的理論,而把無類型 lambda 演算看作它的只有一個類型的特殊情況。
)指示匿名函式抽象的一種有類型的形式化。有類型 lambda 演算是基礎程式語言並且是有類型的函式式程式語言如 ML 和 Haskell 和更間接的指令式程式語言的基礎。它們通過 Curry-Howard同構密切關聯於直覺邏輯並可以被認為是範疇的類的內部語言,比如簡單類型 lambda 演算是笛卡爾閉範疇(CCC)的語言。有類型 lambda 演算被看作無類型lambda演算的精細化。更現代的觀點把有類型 lambda 演算看做更基礎的理論,而把無類型 lambda 演算看作它的只有一個類型的特殊情況。
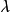
簡單類型 lambda 演算(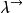 )是連線詞只有
)是連線詞只有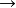 (函式類型)的有類型 lambda 演算。這使它成為規範的、在很多方面是最簡單的有類型 lambda 演算的例子。簡單類型也被用來稱呼對簡單類型 lambda 演算的擴展比如積、陪積或自然數(系統 T)甚至完全的遞歸(如PCF)。相反的,介入了多態類型(如系統F)或依賴類型(如邏輯框架)的系統不被當作是簡單類型。簡單類型 lambda 演算最初由阿隆佐·邱奇在 1940 年介入來嘗試避免無類型 lambda 演算的悖論性使用。
(函式類型)的有類型 lambda 演算。這使它成為規範的、在很多方面是最簡單的有類型 lambda 演算的例子。簡單類型也被用來稱呼對簡單類型 lambda 演算的擴展比如積、陪積或自然數(系統 T)甚至完全的遞歸(如PCF)。相反的,介入了多態類型(如系統F)或依賴類型(如邏輯框架)的系統不被當作是簡單類型。簡單類型 lambda 演算最初由阿隆佐·邱奇在 1940 年介入來嘗試避免無類型 lambda 演算的悖論性使用。
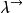
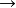
簡單類型 lambda 演算的類型構造自基本類型(或類型變數)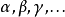 ,給定類型
,給定類型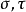 我們能構造
我們能構造 。邱奇只使用了兩個基本類型,
。邱奇只使用了兩個基本類型, 是命題的類型,
是命題的類型, 是個體的類型。這種演算經常只有一個基本類型,通常考慮為
是個體的類型。這種演算經常只有一個基本類型,通常考慮為 。
。
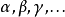
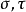




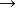
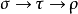
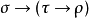
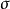
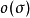
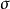
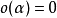
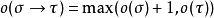
依賴類型
在計算機科學和邏輯中,依賴類型(或依存類型,dependent type)是指依賴於值的類型,其理論同時包含了數學基礎中的類型論和計算機編程中用以減少程式錯誤的類型系統兩方面。在 Per Martin-Löf 的直覺類型論中,依賴類型可對應於謂詞邏輯中的全稱量詞和存在量詞;在依賴類型函式式程式語言如 ATS、Agda、Dependent ML、Epigram、F* 和 Idris 中,依賴類型系統通過極其豐富的類型表達能力使得程式規範得以藉助類型的形式被檢查,從而有效減少程式錯誤。
依賴類型的兩個常見實例是依賴函式類型(又稱依賴乘積類型、Π-類型)和依賴值對類型(又稱依賴總和類型、Σ-類型)。一個依賴類型函式的返回值類型可以依賴於某個參數的具體值,而非僅僅參數的類型,例如,一個輸入參數為整型值n的函式可能返回一個長度為n的數組;一個依賴類型值對中的第二個值可以依賴於第一個值,例如,依賴類型可表示這樣的類型:它由一對整數組成,其中的第二個數總是大於第一個數。
依賴類型增加了類型系統的複雜度。由於確定兩個依賴於值的類型的等價性需要涉及具體的計算,若允許在依賴類型中使用任意值的話,其類型檢查將會成為不可判定問題;換言之,無法確保程式的類型檢查一定會停機。由於Curry-Howard同構揭示了程式語言的類型論與證明論的直覺邏輯之間的緊密關聯性,以依賴類型系統為基礎的程式語言大多同時也作為構造證明與可驗證程式的輔助工具而存在,如 Coq 和 Agda(但並非所有證明輔助工具都以類型論為基礎);近年來,一些以通用和系統編程為目的的程式語言被設計出來,如 Idris。