1965年蘇聯數學家Kolmogolov提出利用信源序列的結構特性來編碼。而兩位以色列研究者J.Ziv和A.Lempel獨闢蹊徑,完全脫離Huffman及算術編碼的設計思路,創造出了一系列比Huffman編碼更有效,比算術編碼更快捷的通用壓縮算法。將這些算法統稱為LZ系列算法。
基本介紹
- 中文名:LZ編碼
- 時間:1965年
- 提出:Kolmogolov
- 性質:更快捷的通用壓縮算
算法舉例,改進,
算法舉例
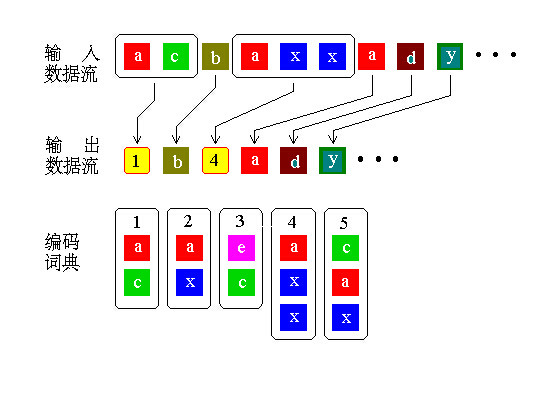
設信源符號集A={a1,a2,…,aK}共K個符號,設輸入信源符號序列為u=(u1,u2,…,uL)編碼是將此序列分成不同的段。分段的規範為:儘可能取最少個相連的信源符號,並保證各段都不相同。
開始時,先取一個符號作為第一段,然後繼續分段。若出現與前面相同的符號時,就再取緊跟後面的一個符號一起組成一個段,使之與前面的段不同。這些分段構成字典。當字典達到一定大小後,再分段時就應查看有否與字典中的短語相同,若有重複就添加符號,以便與字典中短語不同,直至信源序列結束。
編碼的碼字由段號加一個符號組成。設u構成的字典中的短語共有M(u)個。若編碼為二元碼,段號所需碼長n=「log M(u)「(註:代表上取整符號),每個符號需要的碼長為「log K「。單符號的碼欄位號為0,非單字元的碼欄位號為除最後一個符號外字典中相同短語的段號。
例如,設U={a1,a2,a3,a4},信源序列為a1,a3,a2,a3,a2,a4,a3,a2,a1,a4,a3,a2,a1,共13位,字典如表所示:
表1 編碼字典
段號 | 短語 | 編碼 |
1 | a1 | 00000 |
2 | a3 | 00010 |
3 | a2 | 00001 |
4 | a3a2 | 01001 |
5 | a4 | 00011 |
6 | a3a2a1 | 10000 |
7 | a4a3 | 10110 |
8 | a2a1 | 01100 |
表2 符號編碼表
a1 | a2 | a3 | a4 |
00 | 01 | 10 | 11 |
表1中,8個短語使用3bit可以表示段號。每個信源符號使用2bit表示,因此,一個短語使用5bit。
LZ編碼的編碼方法非常簡捷,解碼也很簡單,可以一邊解碼一邊建立字典,只要傳輸字典的大小,無需傳輸字典本身。當編碼的信源序列增長時,編碼效率會提高,平均碼長會逼近信源熵。
改進
Ziv和Lempel於1977年提出了LZ77算法[Ziv & Lempel (1977)]。1978年,二人又提出了改進算法,後被命名為LZ78[Ziv & Lempel (1978)]。1984年,T.A.Welch提出了LZ78算法的一個變種,即LZW算法[ Welch (1984)]。1990年後,T.C.Bell等人又陸續提出了許多LZ系列算法的變體或改進版本[ Bell 等(1990)]。
LZ系列算法用一種巧妙的方式將字典技術套用於通用數據壓縮領域,而且,可以從理論上證明LZ系列算法同樣可以逼近信息熵的極限。