L1自適應控制

由被控對象、狀態預測器、自適應律、控制律等組成的一種控制。

基本介紹

• 中文名：L1自適應控制

L1自適應背景

L1自適應控制算法是一種快速魯棒的自適應控制。該算法實際上是模型參考自適應控制進行了改進，通過在控制律設計環節添加了一個低通濾波器，保證了控制律和自適應律設計的分離。

L1自適應系統機構

L1自適應控制系統可分為：被控對象、狀態預測器、自適應律、控制律

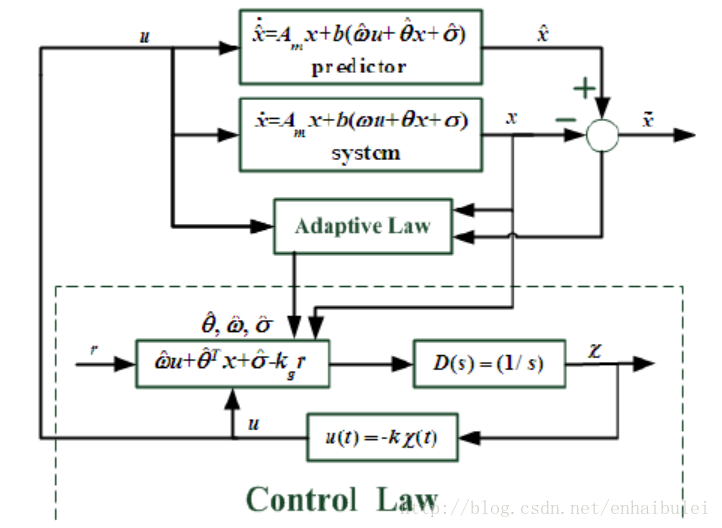L1自適應控制系統

• 被控對象：採用狀態空間形式表達，其中w、θ等為參數不確定性
  
• 狀態預測器：數學模型如上圖所示，其中x，w等對應的是被控對象當中的估計值。當時間趨於無窮時，被控對象將與狀態預測器具有一致的動力學特性，估計偏差在李雅普諾夫意義下穩定
  
• 自適應律：以狀態預測器和被控對象之間的誤差為主要輸入，保證其在李雅普諾夫意義下穩定而得到了對不確定性參數的估計
  
• 控制律：包括兩個部分
  1、與狀態預測器相匹配的對參考輸入的重構；
  2、低通濾波環節。
  

自適應控制理論簡介

自適應控制的研究對象是具有一定程度不確定性的系統，這裡所謂的“不確定性”是指描述被控對象及其環境的數學模型不是完全確定的，其中包含一些未知因素和隨機因素。

任何一個實際系統都具有不同程度的不確定性，這些不確定性有時突出在系統內部，有時突出在系統的外部。從系統內部來講，描述被控對象的數學模型的結構和參數，設計者事先並不一定能準確知道。作為外部環境對系統的影響，可以等效地用許多擾動來表示。這些擾動通常是不可預測的。此外，還有一些測量時產生的不確定因素進入系統。面對這些客觀存在的各式各樣的不確定性，如何設計適當的控制作用，使得某一指定的性能指標達到並保持最優或者近似最優，這就是自適應控制所要研究解決的問題。

自適應控制和常規的反饋控制和最優控制一樣，也是一種基於數學模型的控制方法，所不同的只是自適應控制所依據的關於模型和擾動的先驗知識比較少，需要在系統的運行過程中去不斷提取有關模型的信息，使模型逐步完善。具體地說，可以依據對象的輸入輸出數據，不斷地辨識模型參數，這個過程稱為系統的線上辯識。隨著生產過程的不斷進行，通過線上辯識，模型會變得越來越準確，越來越接近於實際。既然模型在不斷的改進，顯然，基於這種模型綜合出來的控制作用也將隨之不斷的改進。在這個意義下，控制系統具有一定的適應能力。比如說，當系統在設計階段，由於對象特性的初始信息比較缺乏，系統在剛開始投入運行時可能性能不理想，但是只要經過一段時間的運行，通過線上辯識和控制以後，控制系統逐漸適應，最終將自身調整到一個滿意的工作狀態。再比如某些控制對象，其特性可能在運行過程中要發生較大的變化，但通過線上辯識和改變控制器參數，系統也能逐漸適應。

常規的反饋控制系統對於系統內部特性的變化和外部擾動的影響都具有一定的抑制能力，但是由於控制器參數是固定的，所以當系統內部特性變化或者外部擾動的變化幅度很大時，系統的性能常常會大幅度下降，甚至是不穩定。所以對那些對象特性或擾動特性變化範圍很大，同時又要求經常保持高性能指標的一類系統，採取自適應控制是合適的。但是同時也應當指出，自適應控制比常規反饋控制要複雜的多，成本也高的多，因此只是在用常規反饋達不到所期望的性能時，才會考慮採用。

狀態預測器

• 含有參數不確定參數的被控對象數學模型可建立為：
  

x˙=Ax+Bu+σ′

其中A,B,σ表示系統的不確定性，其中A表示被控對象本身結構的不確定性，B表示輸入引起的不確定性，而σ表示系統存在的擾動，與模型參考自適應控制系統設計類似

• 將被控對象轉換為控制系統的期望輸出表達
  數學描述為：
  

x˙=Ax+Bu+σ′

其中Am滿足霍爾維茨條件即滿足穩定條件，r′=wu+θx+σ
對應可知，A=Am+bθ，B=bw，σ=bσ′

• 狀態預測器設計
  狀態預測器是為了被控對象的不確定參數進行估計，其與被控對象具有一致的數學表達。則狀態預測器建模為：
  x^˙=Amx^+b(w^u+θ^x+σ^)
  將被控對象與狀態預測器相減可得，由參考輸入$u$到誤差$\tilde{x}$的狀態表達式為：
  

x~˙=Amx~+b(w~u+θ~x+σ~)

為了保證上式是漸進穩定的，寫出誤差方程的能量函式：

V=12x~TPx~+12Γ−1(w~Tw~+θ~Tθ~+σ~Tσ~)

狀態預測器設計

其中Γ為系統的自適應增益，對上式求導，寫出能量函式導數。則可證明誤差方程在李雅普諾夫意義下穩定。

自適應律設計

自適應律設計部分，通過對估計參數確定其數學表達，保證誤差方程在李雅普諾夫意義穩定，即對李雅普諾夫導數為負定。

w^=−Γ∫u(Pb)Tx~dt

θ^=−Γ∫x(Pb)Tx~dt

σ^=−Γ∫(Pb)Tx~dt

上式為自適應律部分，其為對不確定參數的估計，並保證了誤差方程在李雅普諾夫意義下穩定

控制律設計

• 對控制系統進行控制律設計，控制律環節輸入為u`，輸出為r的數學表達，其保證了輸入到狀態預測器輸出是無穩定誤差的（即輸出可穩定的跟蹤輸入信號）：
  

狀態預測方程（輸入到輸出的傳遞函式）為：

y~=c(sI−Am)−1b(w~u+θ~x+σ~)

當時間趨於無窮時，可達到：

y~=−cA−1mb(w^u+θ^x+σ^)

為保證y^=r則可得：

u=1w^(−1cA−1mbr−θ^x−σ^)

設計低通濾波器，並用L1小增益定理證明穩定性

設計低通濾波器D(s)=1s,對低通濾波器頻寬k設計，為保證閉環控制系統滿足L1小增益定理。

小增益定理：反饋系統中，u1 u2為系統的輸入；y1 y2為系統的輸出； e1 e2為誤差信號；H1 H2為系統本身的特性。當H1 H2的L1範數增益乘積小於1時，系統滿足內穩定條件

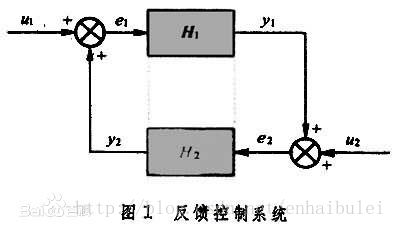反饋控制系統

控制性能分析

控制律設計保證了輸入到y^的穩定性，需要分析輸入到系統輸出的穩態性能

結論：系統誤差的L無窮範數的平方與控制系統自適應參數成反比，當自適應參數足夠大時，系統誤差在任意時刻趨近於0。