彈塑性斷裂力學中一個與路徑無關的積分,是1967由Cherepanov和1968由美國的J.R.賴斯年分別獨立提出的,可作為裂紋或缺口頂端的應變場的平均度量。
基本介紹
- 中文名:J積分
- 外文名:J integral
- 提出者:Cherepanov和J.R.Rice
- 提出時間:1967和1968
J積分簡介
J積分定義
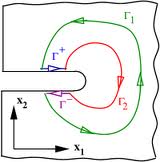 J
J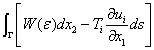 j 積分
j 積分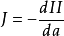
彈塑性斷裂力學中一個與路徑無關的積分,是1967由Cherepanov和1968由美國的J.R.賴斯年分別獨立提出的,可作為裂紋或缺口頂端的應變場的平均度量。
 J
J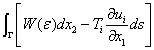 j 積分
j 積分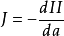
彈塑性斷裂力學中一個與路徑無關的積分,是1967由Cherepanov和1968由美國的J.R.賴斯年分別獨立提出的,可作為裂紋或缺口頂端的應變場的平均度量。...
臨界J積分是指含裂紋構件中的J積分值達到斷裂的臨界狀態時的值,可稱為平面應變條件下裂紋J積分的臨界值,符號為這是斷裂力學J積分理論中所用斷裂判據,也是材料斷裂...
迴路即通過負載再重新流回到電源那裡。積分是微積分學與數學分析里的一個核心概念。在高數中,迴路積分就是當被積函式為封閉曲線,沿著迴路進行積分。若是在二維平面...
材料的J積分阻力值隨裂紋擴展量△a的變化曲線稱為J阻力曲線。大多數韌性材料啟裂後,裂紋尖端的奇異性要比啟裂前的奇異性弱得多,要使裂紋持續擴展,就需要不斷...
J控制裂紋擴展是指在斷裂力學J積分理論中,用J來分析裂紋亞臨界擴展過程需滿足一定的限制條件,滿足這些條件的裂紋擴展為J控制裂紋擴展。...
J積分法是彈塑性斷裂力學的一種基本方法,得到很大的發展。在彈塑性斷裂力學中的主要問題是確定一個能定量表征裂紋尖端應力、應變場強度的參量,它既能易於計算出來,...
6. 楊曉翔,匡震邦, “用J積分法計算壓電材料平面應變問題的能量釋放率及強度因子KⅠ, KⅡ和KⅣ”, 《西安交通大學學報》,1997年第2期。...
這種方法可以計算J積分,應力強度因子等常用的斷裂力學參數裂尖及奇異性定義在interaction-special,先定義crack,定義好裂尖及方向,然後在singularity選擇:midside node ...
8.4 擴展裂紋與J積分 參考文獻 第9章 疲勞裂紋擴展 9.1 等幅載荷下裂紋擴展 9.2 影響疲勞裂紋擴展的因素 9.3 裂紋閉合效應 9.4 疲勞裂紋擴展門檻值確定 9.5 ...
