“遞歸濾波器”。遞歸濾波器,也就是IIR數字濾波器,顧名思義,具有反饋。
基本介紹
特點
區別
設計
3.1 IIR數字濾波器的設計過程
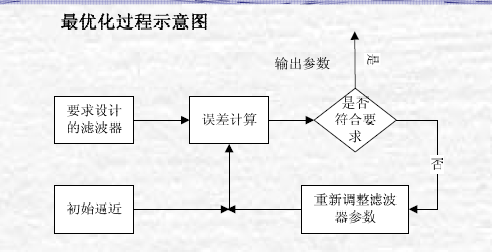 最最佳化過程示意圖
最最佳化過程示意圖3.3 IIR數字濾波器的間接設計法
 模擬轉數字
模擬轉數字
“遞歸濾波器”。遞歸濾波器,也就是IIR數字濾波器,顧名思義,具有反饋。
 最最佳化過程示意圖
最最佳化過程示意圖 模擬轉數字
模擬轉數字“遞歸濾波器”。遞歸濾波器,也就是IIR數字濾波器,顧名思義,具有反饋。...... “遞歸濾波器”。遞歸濾波器,也就是IIR數字濾波器,顧名思義,具有反饋。...
數字濾波器是由數字乘法器、加法器和延時單元組成的一種算法或裝置。數字濾波器的功能是對輸入離散信號的數字代碼進行運算處理,以達到改變信號頻譜的目的。...
套用最廣的是線性、時不變數字濾波器數字濾波其他分類 編輯 從空域上分,可以分為有限數字濾波FIR、無限數字濾波IIR和自適應濾波 [3] 。...
《數字濾波器原理及套用(藉助Matlab)》是2013年9月國防工業出版社出版的圖書,作者是程建華、袁書明、弗雷德 J. 泰勒。...
《數字濾波器原理及套用》是2013年7月1日由國防工業出版社出版的圖書,作者是泰勒 (Taylor F.J.)。...
有限衝激回響數字濾波器(finite impulse re¬sponse digital filter) 數字濾波器的單位衝激回響h(n)只含有有限個非零樣值的一類濾波器,簡記為FIR。它的一般...
第1章,介紹離散時間信號和離散時間系統的基本理論; 第2章,討論DFT的原理及快速算法; 第3章,介紹FIR和IIR數字濾波器的基本結構以及有限字長效應; 第4章,介紹FIR...
無限衝激回響數字濾波器是對單位衝激的輸入信號的回響為無限長序列的數字濾波器。可分為一維、二維或多維無限衝激回響數字濾波器。...
6.7IIR數字濾波器的設計實踐6.7.1模擬濾波器設計問題6.7.2巴特沃思濾波器6.7.3切比雪夫濾波器6.7.4橢圓濾波器6.7.5IIR數字濾波器設計實例...
用軟體來識別有用信號和干擾信號,並濾除干擾信號的方法叫軟體濾波。...11、IIR 數字濾波器A. 方法:確定信號頻寬, 濾之。 Y(n) = a1*Y(n-1)...
《數字濾波器設計及工程套用》是2009年江蘇大學出版社出版的圖書,作者是宋壽鵬。...... 5.5 IIR濾波器階數估計5.5.1 巴特沃斯濾波器階數估計5.5.2 切比雪夫...
《數字濾波器的MATLAB與FPGA實現》是2012年電子工業出版社出版的圖書,作者是杜勇。本書詳細闡述了數字濾波器的實現原理、結構、方法及仿真測試過程,並通過大量工程...
6.1 數字濾波器的基本概念6.2 模擬濾波器的設計6.3 用脈衝回響不變法設計IIR數字低通濾波器6.4 用雙線性變換法設計IIR數字低通濾波器...
第3章 IIR型數字濾波器的設計3.1 典型模擬低通濾波器3.2 模擬濾波器至數字濾波器的變換3.3 IIR型數字濾波器的設計過程和頻率變換...
第6章 IIR數字濾波器設計第7章 FIR數字濾波器設計第8章 多採樣率數位訊號處理第9章 基於MATLAB的通信信號處理第10章 基於MATLAB的語言信號處理...
6數字濾波器設計6.1濾波器概述6.2典型模擬濾波器設計簡介6.3無限衝激回響(IIR)數字濾波器設計6.4有限衝激回響(FIR)數字濾波器設計7數位訊號處理的硬體實現...
設計濾波器時,通常給定的幅度特性是分段恆定的、且在頻帶的邊界有不連續點。逼近這樣的特性,需用無限衝激回響(IIR)數字濾波器。為採用有限衝激回響(FIR)實現,...
