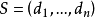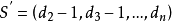Havel-Hakimi算法是圖論中解決圖形實現問題的算法。 也就是說,它回答了以下問題:給定一個非負整數的有限列表,是否有一個簡單的圖形,使得它的度序列恰好是這個列表。 這裡,“度序列”是一個數字列表,對於圖的每個頂點,它表示它有多少個鄰居。 對於肯定答案,整數列表稱為圖形。 該算法構造一個特殊的解決方案,如果存在或證明一個人找不到肯定的答案。 這種結構基於遞歸算法。 該算法由Havel(1955)出版,後來由Hakimi(1962)出版。
基本介紹
- 中文名:Havel–Hakimi算法
- 外文名:Havel–Hakimi algorithm
介紹,算法,代碼,
介紹
1,Havel-Hakimi定理主要用來判定一個給定的序列是否是可簡單圖化的。
2,首先介紹一下度序列:若把圖 G 所有頂點的度數排成一個序列 S,則稱 S 為圖 G 的度序列。
3,一個非負整數組成的有限序列如果是某個無向圖的序列,則稱該序列是可簡單圖化的。
4,判定過程:(1)對當前數列排序,使其呈遞減,(2)從S[2]開始對其後S[1]個數字-1,(3)一直循環直到當前序列出現負數(即不可簡單圖化的情況)或者當前序列全為0 (可簡單圖化)時退出。
5,舉例:序列S:7,7,4,3,3,3,2,1 刪除序列S的首項 7 ,對其後的7項每項減1,得到:6,3,2,2,2,1,0,繼續刪除序列的首項6,對其後的6項每項減1,得到:2,1,1,1,0,-1,到這一步出現了負數,因此該序列是不可簡單圖化的。
算法
Havel–Hakimi算法基於以下定理。
如果給定的序列 是可簡單圖化的,那么算法最多運行
是可簡單圖化的,那么算法最多運行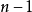 次賦值
次賦值 。注意每次賦值後可能需要重新對序列排序。當
。注意每次賦值後可能需要重新對序列排序。當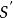 全部為零時,算法停止。在每一步中,如果序列可簡單圖化,就從
全部為零時,算法停止。在每一步中,如果序列可簡單圖化,就從 向
向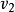 ,
,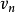 各引出一條邊,即{
各引出一條邊,即{ ,
, },{
},{ ,
, },{
},{ ,
,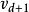 },然後令
},然後令 約化為
約化為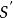 。如果在任何一步中,序列
。如果在任何一步中,序列 無法約化為非負整數序列
無法約化為非負整數序列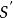 ,算法就給出最開始的
,算法就給出最開始的 不可簡單圖化的結論。
不可簡單圖化的結論。

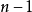


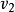
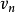





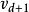

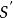

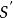

代碼
#include<stdio.h> #include<string.h> #include<algorithm> using namespace std; struct node { int num,e; }x[15]; bool map[15][15]; int cmp(node a,node b) { if(a.num==b.num) return a.e<b.e; return a.num>b.num; } int judge(int n) { int i,num,tmp; while(1){ sort(x+1,x+n+1,cmp); if(!x[1].num) return 1;//數組全為 0 的情況退出 for(i=2;i<=x[1].num+1;i++){ if(x[i].num>0){ x[i].num--; map[x[1].e][x[i].e]=map[x[i].e][x[1].e]=1; } else return 0; } x[1].num=0; } } int main() { int n,t,i,j; bool flag; scanf("%d",&t); while(t--){ scanf("%d",&n); for(i=1;i<=n;i++){ scanf("%d",&x[i].num); x[i].e=i; } memset(map,0,sizeof(map)); flag=judge(n); if(flag){ printf("YES/n"); for(i=1;i<=n;i++){ for(j=1;j<=n;j++) printf(j==1?"%d":" %d",map[i][j]); printf("/n"); } } else printf("NO/n"); if(t) printf("/n"); } return 0; }