基本介紹
- 中文名:排頭阻塞
- 外文名:Head-of-line blocking
- 英文縮寫:HOL
- 產生原因:先進先出(FIFO)的輸入佇列
發生原因
模型簡介

性能損失
總體性能損失


(2)數據包到達每個輸入時相互是獨立的,與其他輸入無關;
(3)所有輸入連線埠的數據包具有相同的到達率且目的地是均勻地分布在所有輸出;
(4)到達的數據包是固定的和相等的長度;
(5)N足夠大(N->∞)。
性能損失分析


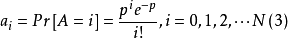










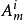
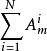

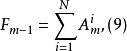


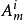






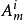

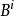

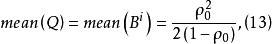
另一方面,利用式(11)可得:


解決方案
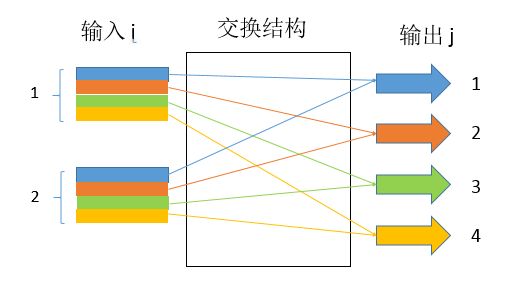
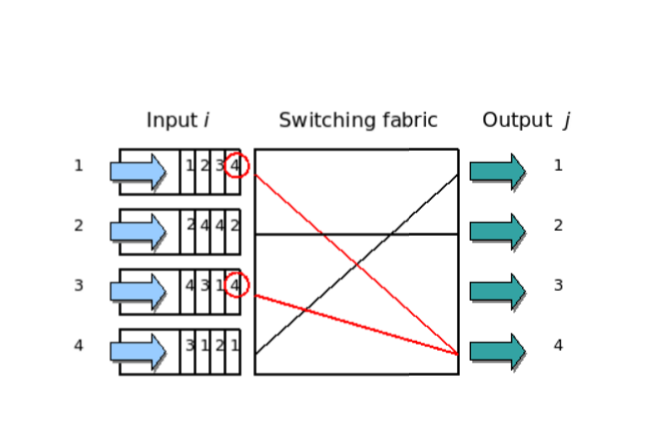





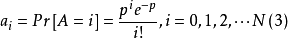










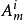
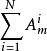

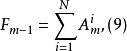


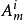






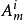

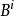

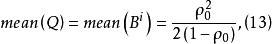



排頭阻塞(Head-of-line blocking, HOL)是一種出現在快取式通信網路交換中的一種現象。交換結構通常由快取式先進先出輸入連線埠、一個交換結構以及快取式先進先出...
Holzinger公式(Holzinger formula)(1929)是根據遺傳度越高的疾病,一卵雙生的患病一致率與二卵雙生患病一致率相差越大而建立的。一卵雙生(monozygotic twin,MZ)是由...
Udomlarb Tanaphol,泰國籍足球運動員。...... Udomlarb Tanaphol .Euro Sport[引用日期2014-10-03] 詞條標籤: 人物 V百科往期回顧 詞條統計 瀏覽次數:次 編輯...
1. June Holstrum ..[引用日期2014-04-11] 詞條標籤: 娛樂人物 , 人物 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:4次歷史版本 最近更新: 創建者:肥...
Microsoft HoloLens 是微軟首個不受線纜限制的全息計算機設備,能讓用戶與數字內容互動,並與周圍真實環境中的全息影像互動。該產品於台北時間2015年1月22日凌晨發布。...
Holmuradov Akmal,烏茲別克斯坦籍足球運動員。...... Holmuradov Akmal,烏茲別克斯坦籍足球運動員。 外文名 Holmuradov Akmal 國籍 烏茲別克斯坦 出生日期 1989年1...
Belhol,阿爾及利亞籍運動員。...... Belhol,阿爾及利亞籍運動員。外文名 Belhol 國籍 阿爾及利亞 所屬運動隊 ESMostaganem 職業 運動員 ...
Drago Nusshol是一名演員,代表作品有《永不止步》、《西瓜之旅》等。...... Drago Nusshol是一名演員,代表作品有《永不止步》、《西瓜之旅》等。...
Holpert Jan是一名德國籍運動員,場上位置是Athlete。...... Holpert Jan是一名德國籍運動員,場上位置是Athlete。外文名 Holpert Jan 國籍 德國 出生日期 1968年...
Valerie Holvick ..[引用日期2014-01-03] 詞條標籤: 人物 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:2次歷史版本 最近更新: 創建者:精品0074猜...
Scott Holdredge是一名藝術指導,參與作品有《晚宴》、《長子》等。...... Scott Holdredge是一名藝術指導,參與作品有《晚宴》、《長子》等。外文名 Scott Holdredge...
E.C. Holkin是一名演員,主要作品有《有閒階級》。...... E.C. Holkin是一名演員,主要作品有《有閒階級》。外文名 E.C. Holkin 職業 演員 代表作品 有...
Holcik H,斯洛伐克籍足球運動員。...... Holcik H .Euro Sport[引用日期2014-05-18] 詞條標籤: 人物 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:1次歷史...
B**ch be humble hol' up b**ch Sit down hol' up lil' hol' up Be humble hol' up b**ch Sit down sit down lil' sit down lil' Be humble h...
Holwing Storm 在騎乘時所有武器傷害提升一定比例。 Keen Eyed 使用弓箭暗殺敵人後回復一定比例的專注值。 Renewed 在使用弓箭擊殺敵人後有一定幾率回復5 點生命值。...
虛擬輸出佇列VoQ(Virtual Output Queue)是網路設備接口在無擁塞的情況下,防止HOL阻塞(Head of Line Blocking)的佇列技術。...
海綿動物 ,但在深海中更常見。其骨骼為複雜的矽質骨針,基本形態呈六放形。屬和種包括:泡沫海綿、維納斯花籃(EuplectellaAspergillum)、Holascus、圍線海綿。鈣質...
