GCR代數

設𝒜為C*代數，如果對𝒜的每個不可約表示(H,π)，都有π(𝒜)⊂𝒦(H)（即H上緊運算元全體），則稱𝒜是CCR代數。

基本介紹

• 中文名：GCR代數
• 外文名：GCR algebra
• 適用範圍：數理科學

簡介

CCR代數

CCR代數是具有緊表示的C*代數，每個有限維C*代數都是CCR代數。

設𝒜為C*代數，如果對𝒜的每個不可約表示(H,π)，都有π(𝒜)=𝒦(H)（即H上緊運算元全體），則稱𝒜是CCR代數。

定義

如果把定義中的條件“π(𝒜)=K(H)”放寬為“π(𝒜)⊂𝒦(H)”，就得到GCR代數的概念。

C*代數

C*代數是一類重要的巴拿赫∗代數。設R是巴拿赫∗代數，如果對R的每個元都有||x*x||=||x||²成立，則稱R為C*代數。

當C*代數有單位元e時，則||e||=1自動成立。若R沒有單位元，做擴張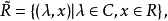並在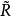中引人範數||(λ,x)||=||L(λ,x)||，則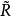成為有單位元(1,0)的C*代數。這裡L(λ₀,x₀)表示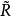上運算元(λ,x)→(λ₀,x₀)(λ,x)。

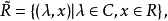
C*代數是蓋爾范德（部分與奈瑪克合作）等於20世紀40年代提出並做了系統而精美的研究，它在抽象調和分析、量子物理等領域中有重要作用。