獨立成分分析(Independent Component Analysis,ICA)是近年來提出的非常有效的數據分析工具,它主要用來從混合數據中提取出原始的獨立信號。它作為信號分離的一種有效方法而受到廣泛的關注。
基本介紹
- 中文名:獨立成分分析
- 外文名:(Independent Component Analysis
- 優點:收斂速度快
- 廣泛套用:信號處理領域
摘要,FastICA簡介,優點,FastICA算法的說明,
摘要
在諸多ICA算法中,固定點算法 (也稱FastlCA)以其收斂速度快、分離效果好被廣泛套用於信號處理領域。該算法能很好地從觀測信號中估計出相互統計獨立的、被未知因素混合的原始信號。
FastICA簡介
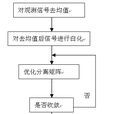
近幾年出現了一種快速ICA算法(Fast ICA),該算法是基於定點遞推算法得到的,它對任何類型的數據都適用,同時它的存在對運用ICA分析高維的數據成為可能。又稱固定點(Fixed-Point)算法,是由芬蘭赫爾辛基大學Hyvärinen等人提出來的。是一種快速尋優疊代算法,與普通的神經網路算法不同的是這種算法採用了批處理的方式,即在每一步疊代中有大量的樣本數據參與運算。但是從分散式並行處理的觀點看該算法仍可稱之為是一種神經網路算法。FastICA算法有基於四階累積量、基於似然最大、基於負熵最大等形式。此外,該算法採用了定點疊代的最佳化算法,使得收斂更加快速、穩健。用流程圖的形式表現算法的流程如圖:
優點
較普通的ICA算法,它具有以下優點:
1)收斂速度快。在 ICA數據模型的假設下,FastICA收斂速度是3次的(或至少是2次的),而普通的ICA算法收斂速度僅僅是線性的。
2)和基於梯度的算法相比,快速定點算法不需要選擇步長參數,說明該算法更加易於使用。
4)FastICA算法的性能能夠通過選擇一個適當的非線性函式g而使其達到最佳化。特別是能得到最小方差的算法。
5)獨立分量可被逐個估計出來,在探索性數據分析里是非常有用的,這類似於做投影追蹤,這在僅需要估計幾個(不是全部)獨立分量的情況下,能極大地減小計算量。
FastlCA算法本質上是一種最小化估計分量互信息的神經網路方法,是利用最大熵原理來近似負熵,並通過一個合適的非線性函式g使其達到最優。這個算法具有很多神經算法里的優點:並行的、分布的、計算簡單、要求記憶體小。如果要估計多個分量。
FastICA算法的說明
1)對觀測信號去均值是ICA算法最基本和最必須的預處理步驟,其處理過程是從觀測中減去信號的均值向量,使得觀測信號成為零均值變數。該預處理只是為了簡化 ICA算法,並不意味著均值不能估計出來。
2)一般情況下所獲得的數據都具有相關性,通常都要求對數據進行初步的白化或球化處理,因為白化處理可去除各觀測信號之間的相關性,從而簡化後續獨立分量的提取過程。通常情況下,數據進行白化處理與不對數據進行白化處理相比,算法的收斂性較好,有更好的穩定性。
簡單地說快速ICA算法通過三步完成:首先,對觀測信號去均值;然後,對去均值後的觀測信號白化處理;前兩步可以看成是對觀測信號的預處理,通過去均值和白化可以簡化ICA算法。最後,獨立分量提取算法及實現流程見流程圖。
FastICA算法的方法輸出向量,在排列順序的時候可能出現顛倒和輸出信號幅度發生變化。這主要是由於ICA的算法存在2個內在的不確定性導致的:
1)輸出向量排列順序的不確定性,即無法確定所提取的信號對應原始信號源的哪一個分量;
2)輸出信號幅度的不確定性,即無法恢復到信號源的真實幅度。
但由於主要信息都包含在輸出信號中,這2種不確定性並不影響其套用。