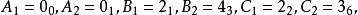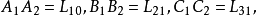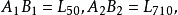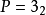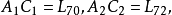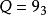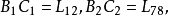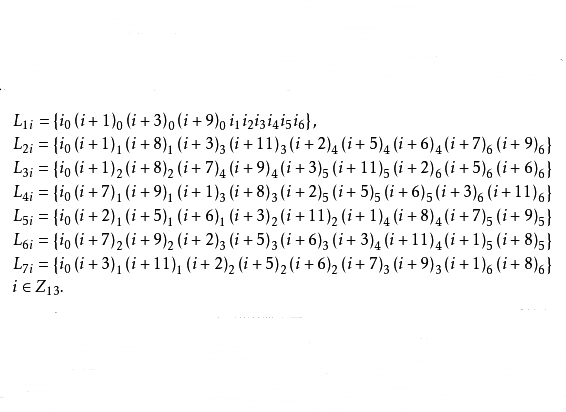Desargues平面

德扎格平面(Desargues plane)是一類射影平面，能使德扎格定理成立的射影平面，德扎格定理斷言：若O，A₁，B₁，C₁，A₂，B₂，C₂是相異點，且OA₁A₂，OB₁B₂，OC₁C₂是相異線，線A₁B₁與A₂B₂交於點C₃，線A₁C₁與A₂C₂交於點B₃，線B₁C₁與B₂C₂交於點A₃，則點A₃，B₃，C₃落在同一條線上，以有限域上3維向量作為齊次坐標所得到的射影平面是德扎格平面，並非所有的射影平面都是德扎格平面，不能使德扎格定理成立的射影平面稱為非德扎格平面。

基本介紹

• 中文名：Desargues平面
• 外文名：Desargues plane
• 所屬學科：數學(組合學）
• 簡介：能使德扎格定理成立的射影平面
• 別稱：德扎格平面

基本介紹

定義Desargues定理成立的射影平面稱德扎格(Desargues)平面。

下面介紹Desargues定理。

Desargues定理是射影幾何中的基本定理之一。對任意素數冪q，Desargues定理在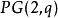中都成立。還將給出Desargues定理不成立的有限射影平面的例子。

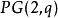
設q為素數冪，以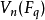表示F_q上的n維向量空間，則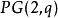便是以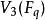中1維子空間為點，2維子空間為線，以子空間的包含關係為關聯關係所得的q階射影平面。設x為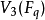中的一個非零向量，用[x]表示由x生成的一維子空間亦即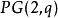中的點，則對任意λ∈ ，顯然有[x]=[λx]，即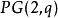中的點與表示此點的非零向量的選取無關。設[x]與[y]為兩個不同的點，則[x]與[y]同時包含在唯一的一條直線L上，此處L由所有滿足下述條件的q+1個點[x]組成：

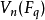
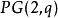
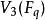
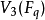
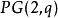
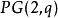
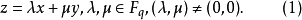
定理1在PG(2，q)中，Desargues定理成立，即設3條不同的直線A₁A₂、B₁B₂、C₁C₂相交於同一點，X為不同A₁、A₂、B₁、B₂、C₁、C₂的一點。又設A₁B₁、A₂B₂，A₁C₁、A₂C₂，B₁C₁、B₂C₂分別交於點P、Q、R，則P、Q、R3點共線。

相關定理

定理2對任意素數冪q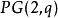，是Desargues平面。

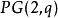
存在非Desargues平面，見下例。

【例1】設n=9，9階射影平面是一個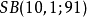。在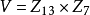上構造一個9階射影平面。為方便計，把V中的元素(i，j)記作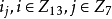，作出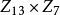上的如下91條直線：

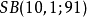
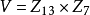
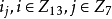
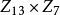
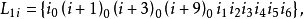
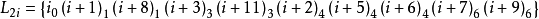
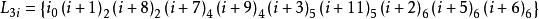
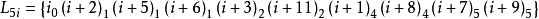
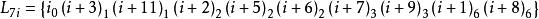
則由這些直線組成Z₁₃×Z₉上的一個9階射影平面π。今證在該平面中Desaugues定理並不成立。因若取

則直線

這3條直線交於點1₀。又直線

因此點；直線

因此；直線

因此點R=2₃。然而過點P、Q的直線為L₆₆，它並不含點R。因此在該平面中Desaugues定理並不成立。