基本介紹
- 中文名:變異係數
- 外文名:Coefficient of Variance
- 公式:C.V.=σ/μ
- 外文縮寫:C.V.
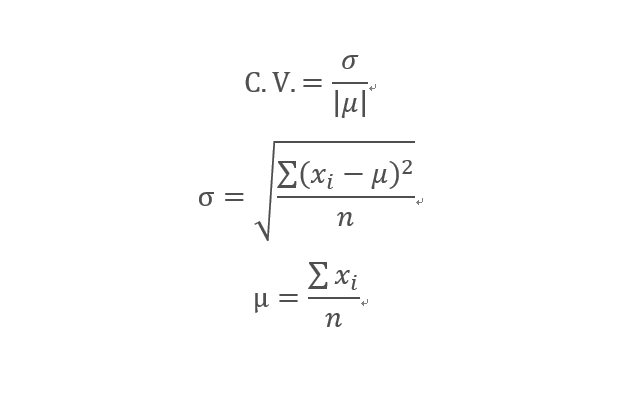
標準差與平均數的比值稱為變異係數,記為C.V(Coefficient of Variance)。用公式表示為:CV=σ/μ。變異係數又稱“標準差率”,是衡量資料中各觀測值變異程度的另...
CV(Curriculum Vitae)是個人簡歷(履歷)的簡稱。和resume相比較,CV通常更加的詳細(一般都要兩頁紙或以上),涵蓋更加全面也比resume更為嚴格。一般用於申請工作、學術...
CV是charactor voice的簡稱,即角色聲音。...... CV是charactor voice的簡稱,即角色聲音。中文名 角色聲音 原版名稱 charactor voice 遊戲平台 PC、PS、XBox 發...
Cv值表示的是元件對介質的流通能力,即:流量係數。具體對於閥門來講,單位時間內、在測試條件中管道保持恆定的壓力,管道介質流經閥門的體積流量,或是質量流量。國外...
CV是一個英文縮寫,意思有簡歷、飛機製造商、計算機病毒、 (基督教《聖經》的)普通譯本、維德角群島、恆定體積等。...
《我們有CV》是由語玩打造的CV選秀綜藝節目,集結了北斗企鵝、光合積木、端木蘇榭等CV社團,致力挖掘中國CV屆的好聲音,讓小眾文化走向大眾視野。 《我們有CV》第...
CV,全稱Coefficient Of Variation。即變異係數。變異係數又稱“標準差率”,是衡量資料中各觀測值變異程度的另一個統計量。當進行兩個或多個資料變異程度的比較時,...
中文網路配音聲優(CV),聲線多變,2009年入圈,現屬於涅槃工作室。代表作品《針鋒對決》、《兩口子的第七年》、《幻生之手》、《狼的誘惑》等。...
cvCvtColor是Opencv里的顏色空間轉換函式,可以實現RGB顏色向HSV,HSI等顏色空間的轉換,也可以轉換為灰度圖像,參數CV_RGB2GRAY是RGB到gray。...
cv 變異係數(coefficient of variation),亦稱離散係數(coefficient of dispersion)或相對偏差(rsd)。中文名 變異係數 外文名 coefficient of variation cv 變異係數(...
CvPoint從CvPoint2D32f轉換 轉換如下:inline CvPoint cvPointFrom32f( CvPoint2D32f point ); CvPoint變體類型 CvPoint2D32fCvPoint2D64f...
cv阿冊編輯 鎖定 阿冊,男,配音演員、歌手,聲音華麗磁性富有質感,不僅有溫暖人心的力量,更有蠱惑人心的魅力,聲音可塑性強,可以駕馭各種角色;歌聲感情豐富、直入人心...
大黃蜂號航空母艦(英文:USS Hornet,舷號:CV-8),是美國海軍隸下的一艘航空母艦,是美國約克城級航空母艦的三號艦。大黃蜂號航空母艦與約克城級前兩艘相比,艦體...
L7805CV是輸出電壓為4.75-5.25V,靜態電流為4.2-8mA的正電壓穩壓器。其輸出電流可達1.5A,不需外接補償元件,內含限流保護電路,防止負載短路燒毀元件。...
很多人誤認為CV(Character Voice)是日本人對聲優的簡稱,甚至有人認為CAST也是聲優,實際上CV只用來標示作品中角色是由哪位配音員來配音的,即角色聲音的意思,並不是...
龜仙人,暱稱:龜娘,又稱小龜,是配音演員、網路歌手、知名網路CV、節目主持人、遊戲解說。原創作品有《哀思》、《Dearest》、《故國》《三生》等。翻唱作品《大王叫...
《超決戰!貝利亞銀河帝國》紅蓮火焰(原CV:關智一) 《城市別動隊》 《赤焰戰場》 《重返17歲》少年邁克(扎克·埃夫隆 飾) 《醜女大翻身》韓相俊(朱鎮模飾) 《叢...
2007年他因擔任《再見!絕望先生》、《高達00》等作品主角的CV而受到矚目,同年開始與小野大輔主持DearGirl~Stories~,於08年憑藉提耶利亞·厄德這一角色獲得第二...
Character Voice指角色聲音,通常簡稱作“CV”,常用於日本動畫。CV(Character Voice)為和製英語,於上世紀八十年代後半由動畫雜誌《Animec》的副編輯長井上申一郎...
