在數位訊號處理中，CIC濾波器是FIR濾波器中最優的一種，其使用了積分，梳狀濾波器級聯的方式。
CIC濾波器由一對或多對積分-梳狀濾波器組成，在抽取CIC中，輸入信號依次經過積分，降採樣，以及與積分環節數目相同的梳狀濾波器。在內插CIC中，輸入信號依次經過梳狀濾波器，升採樣，以及與梳狀數目相同的積分環節。
基本介紹
- 中文名：積分-梳狀級聯濾波器
- 外文名：Cascaded integrator–comb filter
定義,性質,平滑作用,相似產品比較,
定義
CIC濾波器的發明者是 Eugene B. Hogenauer，這是一類使用在不同頻率的數位訊號處理中的濾波器，在內插和抽取中使用廣泛。與大多數FIR濾波器不同的是，它有一個內插或者抽取的結構。
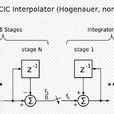
下圖展示了CIC濾波器的結構：
對於CIC濾波器的傳遞函式，可以用下圖中的表達式表示：
下圖展示用matlab中fdatool工具，進行CIC濾波器設計得到的回響曲線，以及相應的參數：
其中R表示升採樣或降採樣的倍數，
M表示每個微分環節延遲的個數，通常為1，有時是2。
N表示積分/梳狀器的個數。
性質
- 線性相位回響
- 僅需延遲，加減法便可實現，不需要乘法，在FPGA等平台上易於實現。
平滑作用
CIC濾波器是滑動平均濾波器的一種有效實現。考慮滑動平均濾波器的一般實現形式，將新的x[n]加到y[n-1]上，並減去上一時間的採樣相加之和。可以用下圖來表示：
上圖中的第二個等式與梳狀（c[n]=x[n]-x[n-RM]）後接積分器（y[n]=y[n-1]+c[n]）對應。常見的CIC濾波器都是將N個相同的梳狀和積分器級聯，並重新排列順序，梳狀和積分器各自放到一起，再排出先後順序即可。可以這樣重新排列是因為兩種結構都是線性時不變的。
由於中間過程的累加，所以使用的數據位長可能需要延長，延長的位數滿足使可能出現的最大位長也不溢出。使用位長的計算公式如下：L=l+N*log2(RM)。以輸入位長為1為例，M=1，降採樣倍數R為16，積分器級數N=3，則應該至少使用1+3*log2(16)=13位的數據，以避免溢出。
相似產品比較
CIC濾波器被套用在變頻過程處理中，FIR濾波器有著多種套用，可以套用在不同採樣頻率的升採樣，降採樣中。CIC濾波器有著低通濾波器的特性，其他的FIR可以呈現低通，高通，帶通等多種特性。和大多數FIR不同的是，CIC的實現只需要用到加減，不需要用到乘法。CIC濾波器會有特定頻率的衰減，其他的FIR濾波器可以在任意頻率衰減。
CIC濾波器比大多數FIR濾波器更加經濟，但也有其不足。在需要少量升/降採樣的場合中，FIR濾波器有其優點，但是如果採樣頻率的變化較大（如10倍以上），實現一個抗混疊的濾波器需要很高的代價，此時CIC 便體現出其優越性。而且如果升/降採樣的倍數發生變化，在數據位長足夠的前提下，僅僅改變升/降採樣環節的倍數即可。
FIR濾波器可以使用定點/浮點數，CIC濾波器只能使用定點數，因為作為遞歸實現的結構，非常依賴梳狀和積分器的零極點相消。CIC濾波器所能提供的濾波器回響形狀非常有限。通過增加極點，可以得到更多的阻帶。但是這樣做也會導致梳狀器和積分器中數據位長的增加。由於CIC濾波器的設計自由度低，實際中很少單獨使用，如果後接一個FIR或IIR校正相位，就會實用得多。
