CES即常數替代彈性(Constant Elasticity of Substitution)是二元函式的一種性質,具有此性質的函式稱為CES函式。
基本介紹
- 中文名:常數替代彈性
- 外文名:Constant Elasticity of Substiution
- 縮略語:CES
定義



套用
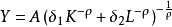









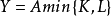


CES即常數替代彈性(Constant Elasticity of Substitution)是二元函式的一種性質,具有此性質的函式稱為CES函式。



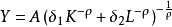









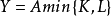


國際消費類電子產品展覽會,簡稱國際消費電子展,常簡稱為CES,每年1月在美國內華達州拉斯維加斯舉行,由消費電子協會贊助。在展覽期間,會有許多產品的預覽或宣布新產品...
CES是Cranial Electrotherapy Stimulation 的英文簡稱,翻譯為經顱微電流刺激療法。 CES是一種可以治療焦慮、抑鬱、失眠及兒童多動症等精神心理相關疾病的非藥物治療...
CES是允許用戶將多個話音和視頻電路仿真流與分組數據復用在一個高速異步轉移模式(ATM)鏈路上傳輸的業務。...
《ces學習法》針對學習中擺脫“題海”困境、達到良好學習效果,提供了“通、點、解、變”的核心理念,對其學習中的通讀、重點的掌握、解決問題、應變創新能力等學習...
2014新ces學習法,全新升級《2014新CES學習法》隆重上市,編委陣容超過100位。眾多名師將畢生教學精華傾囊相授,在原有CES學習法的基礎上,根據最新初高中考試大綱,將...
CES即《劍橋中學英語教程》(Cambridge English for Schools,簡稱劍中或CES),從起始級到四級由低到高共5個級別,是一門學習英語的教程。...
CES展會由美國電子消費品製造商協會(簡稱CEA)主辦,創始於1967年,迄今已有47年歷史,每年1月在世界著名賭城——拉斯維加斯舉辦,是世界上最大、影響最為廣泛的消費...
CES評價模式簡介 編輯 CSE評價模式是以美國洛杉磯加利福尼亞大學評價研究中心(Center for Study of Evaluation)命名的一種評價模式,該中心自20世紀60年代後期以來一直...
CES即常數替代彈性(Constant Elasticity of Substitution)是二元函式的一種性質,具有此性質的函式稱為CES函式。...
2017CES創新大獎是CES和美國消費技術協會主辦的一項大獎賽,2016年8月11日宣布開始徵集參選作品。該年度競賽表彰28個消費科技類別的傑出設計和工程,包括但不限於可...
CES生產函式,即固定替代彈性生產函式。...... CES生產函式中有三個重要的參數A,α和ρ,每個參數都有豐富的經濟學含義,參數的大小對一國的經濟成長和資本使用效率...
美國CES—微電流循環修復術是目前國際神經內科疾病醫學領域非藥物治療焦慮、抑鬱、失眠及兒童相關情緒障礙的最新治療方法。美國CES—微電流循環修復術通過特殊設計波形和...
CES創新設計與工程獎是美國國際消費類電子產品展覽會為表彰消費類電子產品中傑出的設計和工程所設立的獎項。CES創新獎面向29類消費電子產品設獎,以表彰消費類電子產品...
CES是中國東方航空公司的ICAO代碼,運用於國際民用航空組織的空管部門。...... CES是中國東方航空公司的ICAO代碼,運用於國際民用航空組織的空管部門。 詞條標籤: 組織...
CES消費電子展是在美國拉斯維加斯舉辦的國際消費類電子產品的展覽會,通常簡稱CES,CES展由美國電子消費品製造商協會(簡稱CEA)主辦,創始於1967年,每年一月在世界著名...
CES2012是美國拉斯維加斯國際消費電子展覽會(CES)的簡稱,主辦周期是每年一屆。...... CES2012是美國拉斯維加斯國際消費電子展覽會(CES)的簡稱,主辦周期是每年一屆...
CESV是英文單詞Customization+Expansibility+Service+Value的簡稱。它是一個新的網際網路服務概念,意在為客戶提供全方位的優質網際網路服務方案,而不單單只的是注重技術...
CES,全稱contactless excitation system,在電氣工程領域電機勵磁方向中稱為為非接觸式勵磁系統。...
CES(客戶互動銷售(Customer Engagement Selling))編輯 鎖定 本詞條缺少信息欄、名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!客戶互動銷售(Customer ...
2015年CES,在美國拉斯韋加斯拉開帷幕。...... 2015年CES(國際消費類電子產品展)在美國拉斯韋加斯拉開帷幕,CES官方預計今年的展會將吸引超過16萬人次參觀,將有接...
國際消費類電子產品展覽會(International Consumer Electronics Show,簡稱CES),由美國電子消費品製造商協會(簡稱CTA)主辦,旨在促進尖端電子技術和現代生活的緊密結合。該...
2018年國際消費類電子產品展覽會,簡稱2018年國際消費電子展(CES 2018),於2018年1月9日至12日在美國拉斯維加斯舉行。該展覽會為消費類電子技術年展。...
電路仿真業務 CES(Circuit Emulation Service)是ATM(異步轉移模式)網路提供的在質量上可以同常規數字電路相比擬的數字電路業務。在ATM網路邊緣設定電路仿真業務的部件,...
