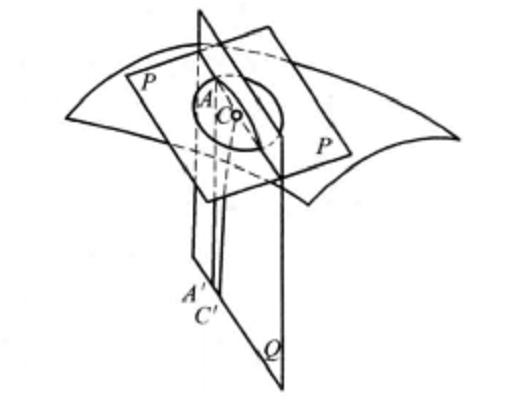
類似於研究線束時的C-曲線的概念,線把的C-曲面為點的軌跡,這些點都線上把內的半線上,且和線把內某一條選定的半線上某一個起點對應,線把內的半線都叫作這個C-曲面的軸。三種類型的線把分別為:聚集線把,分散線把和平行線把。聚集線把的C-曲面為與線把的中心有等距離的點的軌跡,這就是球面,它也可以看成一個圓周繞著它的直徑旋轉所成的曲面。分散線把的C-曲面為與一平面等距離的點的軌跡,它和線把的底面重合,這曲面叫作等距曲面或叫作超球面。平行線把的C-曲面叫作渾球面或叫作極限球面,它是極限圓繞著它的軸旋轉所成的曲面。
基本介紹
- 中文名:C-曲面
- 外文名:C-surface
- 所屬學科:數學
- 所屬學科:羅巴切夫斯基幾何學
- 相關概念:線把,線束,C-曲線等
基本介紹,線把,C-曲面的概念,相關定理,三種線把的C-曲面,聚集線把的C-曲面,分散線把的C-曲面,平行線把的C-曲面,
基本介紹
線把
線把在羅巴切夫斯基空間幾何學裡,和線束在羅巴切夫斯基平面幾何學裡有同樣的作用。
有三種類型的線把存在:
1.聚集線把,指空間所有經過同一點的直線所組成的集合,這點叫作線把的中心。
2.分散線把,指空間所有垂直於同一平面的直線所組成的集合,這平面叫作線把的底面。
如果一平面經過線把的半線,我們便說這平面屬於這線把。
C-曲面的概念
線把的C-曲面為點的軌跡,這些點都線上把內的半線上,且和線把內某一條選定的半線上某一個起點對應,線把內的半線都叫作這個C-曲面的軸。
相關定理
定理1 C-曲面上每一點都可以被取作起點。
定理2 C-曲面的每一條軸都是這曲面的旋轉軸。
 圖1
圖1考慮C-曲面的某一條軸AA',和這曲面的任一點B,點B在軸BB'上,把平面ABA'繞著AA'旋轉任意角後,直線BB'轉到B1B'1的位置,這時,B1B'1依舊屬於C-曲面的各軸所組成的線把,且點B1仍然是A的對應點,即仍是這曲面上的點。因此,C-曲面上任何點,繞著軸AA'旋轉任意角之後,仍然在曲面上,故軸AA'為C-曲面的旋轉軸。屬於線把的每個平面,叫作這線把的C-曲面的直徑面,直徑面和C-曲面的交線,叫作這曲面的直徑面截口。
定理3 C-曲面的一切直徑面截口都是C-曲線,因為截口上一切的點,在這曲面的各軸上互相對應,而這些軸在直徑面截口的平面上組成一個線束。
定理4 直徑面都是C-曲面的對稱平面。
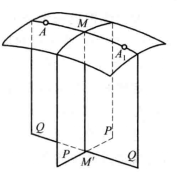 圖2
圖2考慮C-曲面上某點A(圖2),過A作直徑面Q垂直於已給的直徑面P,並設這兩個平面沿著曲面的軸MM’相交。平面Q和曲面相交於C-曲線,且對於軸MM'來說,點A的對稱點A1也在同一C-曲線上,即A1也在曲面上,且關於直徑面P,A1也是點A的對稱點。
我們可說,直徑面截口劃分C-曲面為兩個曲面區靠著這個截口的兩側。
定理5 設A,B,C為C-曲面上的三點,不在同一C-曲線上,那么,我們可以轉移這C-曲面,使曲面上一切的點,經過轉移之後仍在曲面上,而且:
1)點A和C-曲面上預先任意給定的點A1疊合。
2)C-曲線弧AB轉移到預先任意給定的C-曲線弧A1B1。
3)點C和某點C1疊合,C1是在靠著弧A1B1的一個曲面區內,在所有這些轉移的條件下,除了曲面的恆等變換之外,曲面不可能再做進一步的運動。
討論兩軸AA'和A1A'1,的平分線MM'(圖3),直線MM'也是曲面的軸。繞著這平分線把曲面旋轉180°的角,令點A和點A1疊合,經過這轉動之後,如果弧AB不取弧A1B1的位置,那么,繞著軸A1A'1把曲面再轉一次,令AB和已給弧A1B1疊合,此後如果點C不在所給定的曲面區內,則作曲面對於直徑面A1A'1B1的反射映象,把點C帶到所給的曲面區內去。
上述定理的結果也可以表達如下:C-曲面在其本身上有移轉的自由,這個自由的程度,正和平面在其自身上可能轉移的程度一樣。
 圖3
圖3推論 一個C-曲面的所有直徑面截口互相全等,因為移轉曲面可以令它們疊合。
三種線把的C-曲面
分別考慮上面所舉三種類型的線把的C-曲面。
聚集線把的C-曲面
定理1 聚集線把的C-曲面為與線把的中心有等距離的點的軌跡,這就是球面,它也可以看成一個圓周繞著它的直徑旋轉所成的曲面。
事實上,因為曲面上任意兩個對應點所在的半線相交於線把的中心,那么,它們和線把的中心等距離,曲面的直徑面截口上各點也和線把的中心等距離,故截口為一個圓,把這個圓繞直徑旋轉便得已知球面。
分散線把的C-曲面
定理2 分散線把的C-曲面為與一平面等距離的點的軌跡,它和線把的底面重合,這曲面叫作等距曲面或叫作超球面。超球面為超圓繞著它的軸旋轉所成的曲面。
事實上,因為曲面上任意兩個對應點分別在分散線把的兩條半線上,那么,它們和線把的底面等距離。依同理,曲面的一切直徑面截口為超圓,且互相全等,一個超圓繞著它的軸旋轉便得超球面。
平行線把的C-曲面
定理3 平行線把的C-曲面叫作渾球面或叫作極限球面,它是極限圓繞著它的軸旋轉所成的曲面。
事實上,極限球面的直徑面截口上的一切點,在直徑面上一個平行半線束里的半線上互相對應,故為一個極限圓。這極限圓繞著它的軸旋轉便得極限球面。
定理4 一切極限球面全等。
定理5 經過極限球面上一點的平面,或者和它相切,或者和它相交於一圓或一極限圓。