BFGS矩陣(BFGS matrix)尺度矩陣的推廣。
基本介紹
- 中文名：BFGS矩陣
- 外文名：BFGS matrix
.其第k+1次疊代矩陣為
第k+1次疊代矩陣
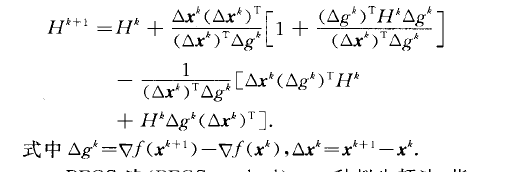
BFGS矩陣(BFGS matrix)尺度矩陣的推廣。
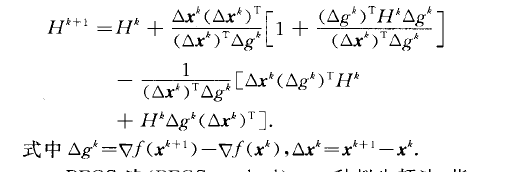
BFGS矩陣(BFGS matrix)尺度矩陣的推廣。.其第k+1次疊代矩陣為...
BFGS法(BFGS method)是一種擬牛頓法，指用BFGS矩陣作為擬牛頓法中的對稱正定疊代矩陣的方法，此法是1970年前後由柏蘿登(C.G.Broyden)、弗萊徹(R.Fletcher)、戈德福布(D.Goldfarb)，以及生納(D.F.Shanno)所研究，故得名，由於BFGS...
Broyden Fletcher Goldfarb Shanno 算法 BFGS 算法同樣是由最佳化中的牛頓法演變而來，N. Amjady 認為 BFGS 算法是準牛頓法中最成功的神經網路算法。準牛頓法中，二階導數的海森矩陣函式將被最小化，不用再對其做其他計算，而是通過分析...
BFGS和DFP公式在形式上是對稱的： 與 對稱， 與 對稱。但是BFGS比DFP更加有效。對稱秩1（SR1）方法 有別於DFP和BFG方法，SR1是一種秩-1更新。它的公式是： 。SR1公式不要求矩陣B_k保持正定性，從而更逼近真實的Hesse矩陣，所以...
8.2 BFGS方法的特性 8.3 SR1方法（秩1校正公式）8.4 SR1校正的特徵 8.5 Broyden族 8.6 收斂性分析 第9章 約束最佳化的基本理論 9.1 可微凸規劃的KKT點 9.2 二階充分條件 9.3 幾個有用的觀察 第10章 線性規劃：單純...
線性獨立與矩陣秩的關係 不難證明若有 階矩陣 如果它的n個行(列)向量是線性獨立的，則該方陣的秩為n，反之如果其n個行向量或n個列向量是線性相關的，則其秩一定小於n，綜上所述，可得定理如下：定理1 n×n階矩陣秩為n的充分...
11.2黑塞矩陣逆矩陣的近似 11.3秩1修正公式 11.4DFP算法 11.5BFGS算法 習題第12章求解線性方程組 12.1最小二乘分析 12.2遞推最小二乘算法 12.3線性方程組的最小範數解 12.4Kaczmarz算法 12.5一般意義下的線性方程組的求解 ...