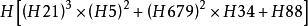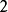Apm定理

Apm定理，是由藝術家炫名在大學二年級時創立的一個數學定理。其主要內容是對整數進位問題的相關性質研究。兩年後，他將其作為自己的畢業論文。

Apm定理提出了一種對整數進位問題的新觀點，通過新定義一個數學運算符號（因編輯關係，此處無法展示這個符號，在此以“H”代替），並根據其屬性，得出相關的結論。

基本介紹

• 中文名：Apm定理
• 外文名：Apm Theorem
• 提出者：炫名
• 提出時間：2010年
• 套用學科：數學

定律定義

H的定義

在十進制中，任意正整數N可表示為：N=,其中為非負個位數字，由此定義運算符號H：將正整數N的各位數上的數字(i=1,2,…,n)相加得到的正整數再做同樣運算，直至所得正整數為個位數為止。

用公式表示為：

若且唯若C為非負個位數時， C=C，其中規定 0=9;

否則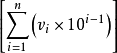， = ，直至得出個位數。

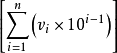
例 （58967156）= （5+8+9+6+7+1+5+6）= （47）= （4+7）= （11）= （1+1）= 2=2

推導過程

推導過程可參考百度文庫詞條“Apm定理”。

Apm定理

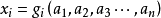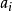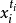設 為只含有加法和乘法運算（不含括弧）的式子，其中 (i=1,2,…,n)為非負整數， 為只含有加法和乘法運算（不含括弧）的式子，對 （其中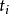 為非負整數，i=1,2,…,n)，有

= ( ， ， ，…， )

=

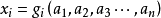
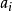
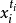
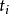
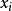
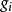
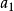
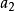
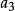
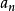
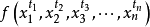
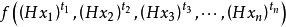
例 ==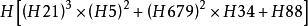