特點
AVL樹本質上還是一棵二叉搜尋樹,它的特點是:
1.本身首先是一棵二叉搜尋樹。
2.帶有平衡條件:每個結點的左右子樹的高度之差的絕對值(平衡因子)最多為1。
也就是說,AVL樹,本質上是帶了平衡功能的二叉查找樹(二叉排序樹,二叉搜尋樹)。
操作
旋轉
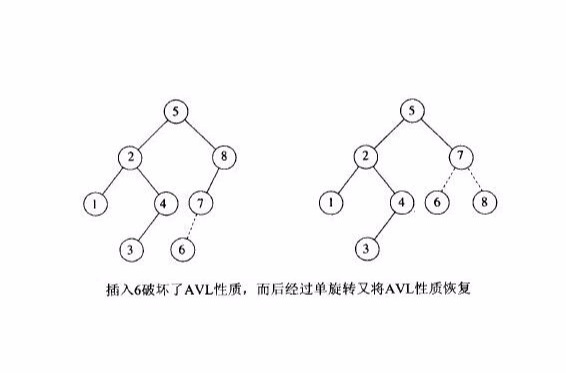
AVL樹的基本操作一般涉及運做同在不平衡的二叉查找樹所運做的同樣的算法。但是要進行預先或隨後做一次或多次所謂的"AVL 旋轉"。
假設由於在
二叉排序樹上插入結點而失去平衡的最小子樹根結點的指針為a(即a是離插入點最近,且平衡因子絕對值超過1的祖先結點),則失去平衡後進行進行的規律可歸納為下列四種情況:
單向右旋平衡處理LL:由於在*a的左子樹根結點的左子樹上插入結點,*a的平衡因子由1增至2,致使以*a為根的子樹失去平衡,則需進行一次右旋轉操作;
單向左旋平衡處理RR:由於在*a的右子樹根結點的右子樹上插入結點,*a的平衡因子由-1變為-2,致使以*a為根的子樹失去平衡,則需進行一次左旋轉操作;
雙向旋轉(先左後右)平衡處理LR:由於在*a的左子樹根結點的右子樹上插入結點,*a的平衡因子由1增至2,致使以*a為根的子樹失去平衡,則需進行兩次旋轉(先左旋後右旋)操作。
雙向旋轉(先右後左)平衡處理RL:由於在*a的右子樹根結點的左子樹上插入結點,*a的平衡因子由-1變為-2,致使以*a為根的子樹失去平衡,則需進行兩次旋轉(先右旋後左旋)操作。
插入
向AVL樹插入可以通過如同它是未平衡的二叉查找樹一樣把給定的值插入樹中,接著自底向上向根
節點折回,於在插入期間成為不平衡的所有節點上進行旋轉來完成。因為折回到根節點的路途上最多有 1.5 乘 log n 個節點,而每次 AVL 旋轉都耗費恆定的時間,插入處理在整體上耗費 O(log n) 時間。 在平衡的的
二叉排序樹Balanced BST上插入一個新的數據元素e的遞歸算法可描述如下: 若BBST為空樹,則插入一個數據元素為e的新結點作為BBST的根結點,樹的深度增1; 若e的關鍵字和BBST的根結點的關鍵字相等,則不進行; 若e的關鍵字小於BBST的根結點的關鍵字,而且在BBST的左子樹中不存在和e有相同關鍵字的結點,則將e插入在BBST的左子樹上,並且當插入之後的左子樹深度增加(+1)時,分別就下列不同情況處理之:BBST的根結點的平衡因子為-1(右子樹的深度大於左子樹的深度,則將根結點的平衡因子更改為0,BBST的深度不變; BBST的根結點的平衡因子為0(左、右子樹的深度相等):則將根結點的平衡因子更改為1,BBST的深度增1; BBST的根結點的平衡因子為1(左子樹的深度大於右子樹的深度):則若BBST的左子樹根結點的平衡因子為1:則需進行單向右旋平衡處理,並且在右旋處理之後,將根結點和其右子樹根結點的平衡因子更改為0,樹的深度不變; 若e的關鍵字大於BBST的根結點的關鍵字,而且在BBST的右子樹中不存在和e有相同關鍵字的結點,則將e插入在BBST的右子樹上,並且當插入之後的右子樹深度增加(+1)時,分別就不同情況處理之。
刪除
從AVL樹中刪除可以通過把要刪除的
節點向下旋轉成一個
葉子節點,接著直接剪除這個葉子節點來完成。因為在旋轉成葉子節點期間最多有 log n個節點被旋轉,而每次 AVL 旋轉耗費恆定的時間,刪除處理在整體上耗費 O(log n) 時間。
查找
在AVL樹中查找同在一般BST完全一樣的進行,所以耗費 O(log n) 時間,因為AVL樹總是保持平衡的。不需要特殊的準備,樹的結構不會由於查詢而改變。(這是與伸展樹查找相對立的,它會因為查找而變更樹結構。)
參考實現
給出一個操作AVLTREE的完整程式 大部分由Peter Brass編寫
#include <iostream.h> #include <math.h>; #include <stdlib.h>; //建立一個整數類型 #define MAXSIZE 512 typedef struct obj_n_t { int obj_key; } obj_node_t; //建立樹結點的基本機構 typedef struct tree_n_t { int key; struct tree_n_t *left,*right; int height;} tree_node_t; //建立堆疊 tree_node_t *stack[MAXSIZE]; //warning!the tree can contain 256 leaves at most! int i=0; //堆疊計數器 //堆疊清空 void stack_clear() { while(i!=0) { stack[i-1]=NULL; i--; }}//堆疊為空int stack_empty(){ return(i==0);}//入棧函式int push(tree_node_t *node){ if(i<MAXSIZE) { stack[i++]=node; return(0); } else return(-1);}//出棧函式tree_node_t *pop(){ if(i>0) return(stack[--i]); else return(0);}//建立get_node函式,用於動態分配記憶體空間tree_node_t *get_node(){ tree_node_t *tmp; tmp=(tree_node_t *)malloc(sizeof(tree_node_t)); return(tmp);}//建立return_node函式,用於釋放記憶體void return_node(tree_node_t *free_node){ free(free_node);}//建立左旋轉函式void left_rotation(tree_node_t *node){ tree_node_t *tmp; int tmp_key; tmp=node->left; tmp_key=node->key; node->left=node->right; node->key=node->right->key; node->right=node->left->right; node->left->right=node->left->left; node->left->left=tmp; node->left->key=tmp_key;}//建立右旋轉函式void right_rotation(tree_node_t *node){ tree_node_t *tmp; int tmp_key; tmp=node->right; tmp_key=node->key; node->right=node->left; node->key=node->left->key; node->left=node->right->left; node->right->left=node->right->right; node->right->right=tmp; node->right->key=tmp_key;}int rebalance(tree_node_t *node){ int finished=0; while(!stack_empty()&&!finished) { int tmp_height,old_height; node=pop(); //back to the root along the search path old_height=node->height; if(node->left->height-node->right->height==2) { if(node->left->left->height-node->right->height==1) {right_rotation(node);node->right->height=node->right->left->height+1;node->height=node->right->height+1;}else{left_rotation(node->left);right_rotation(node);tmp_height=node->left->left->height;node->left->height=tmp_height+1;node->right->height=tmp_height+1;node->height=tmp_height+2;}}else if(node->left->height-node->right->height==-2){if(node->right->right->height-node->left->height==1){left_rotation(node);node->left->height=node->left->right->height+1;node->height=node->left->height+1;}else{right_rotation(node->right);left_rotation(node);tmp_height=node->right->right->height;node->left->height=tmp_height+1;node->right->height=tmp_height+1;node->height=tmp_height+2;}}else{if(node->left->height>node->right->height)node->height=node->left->height+1;elsenode->height=node->right->height+1;}if(node->height==old_height)finished=1;}stack_clear();return(0);}//建立creat_tree函式,用於建立一顆空樹tree_node_t *creat_tree(){tree_node_t *root;root=get_node();root->left=root->right=NULL;root->height=0;return(root); //build up an empty tree.the first insert bases on the empty tree.}//建立find函式,用於查找一個對象obj_node_t *find(tree_node_t *tree,int query_key){tree_node_t *tmp;if(tree->left==NULL)return(NULL);else{tmp=tree;while(tmp->right!=NULL){if(query_key<tmp->key)tmp=tmp->left;elsetmp=tmp->right;}if(tmp->key==query_key)return((obj_node_t*)tmp->left);elsereturn(NULL);}}//建立插入函式int insert(tree_node_t *tree,obj_node_t *new_obj){tree_node_t *tmp;int query_key,new_key;query_key=new_key=new_obj->obj_key;if(tree->left==NULL){tree->left=(tree_node_t *)new_obj;tree->key=new_key;tree->height=0;tree->right=NULL;}else{stack_clear();tmp=tree;while(tmp->right!=NULL){//use stack to remember the path from root to the position at which the new object should be inserted.//then after inserting,we can rebalance from the parrent node of the leaf which pointing to new object to the root node.push(tmp);if(query_key<tmp->key)tmp=tmp->left;elsetmp=tmp->right;}if(tmp->key==query_key)return(-1);else{tree_node_t *old_leaf,*new_leaf;//It must allocate 2 node space in memory.//One for the new one,another for the old one.//the previous node becomes the parrent of the new node.//when we delete a leaf,it will free two node memory spaces as well.old_leaf=get_node();old_leaf->left=tmp->left;old_leaf->key=tmp->key;old_leaf->right=NULL;old_leaf->height=0;new_leaf=get_node();new_leaf->left=(tree_node_t *)new_obj;new_leaf->key=new_key;new_leaf->right=NULL;new_leaf->height=0;if(tmp->key<new_key){tmp->left=old_leaf;tmp->right=new_leaf;tmp->key=new_key;}else{tmp->left=new_leaf;tmp->right=old_leaf;}tmp->height=1;}}rebalance(tmp);return(0);}//建立刪除函式int del(tree_node_t *tree,int key){tree_node_t *tmp,*upper,*other;if(tree->left==NULL)return(-1);else if(tree->right==NULL){if(tree->key==key){tree->left=NULL;return(0);}elsereturn(-1);}else{tmp=tree;stack_clear();while(tmp->right!=NULL){upper=tmp;push(upper);if(key<tmp->key){tmp=upper->left;other=upper->right;}else{tmp=upper->right;other=upper->left;}}if(tmp->key!=key)return(-1);else{upper->key=other->key;upper->left=other->left;upper->right=other->right;upper->height=upper->height-1;return_node(tmp);return_node(other);rebalance(pop());//here must pop,then rebalance can run from the parrent of upper,because upper has become a leaf.return(0);}}}//建立測試遍歷函式int travel(tree_node_t *tree){stack_clear();if(tree->left==NULL)push(tree);else if(tree->left!=NULL){int m=0;push(tree);while(i!=m){if(stack[m]->left!=NULL && stack[m]->right!=NULL){push(stack[m]->left);push(stack[m]->right);}m++;}}return(0);}//建立測試函式int test_structure(tree_node_t *tree){travel(tree);int state=-1;while(!stack_empty()){--i;if(stack->right==NULL && stack->height==0) //this statement is leaf,but also contains an empty treestate=0;else if(stack->left!=NULL && stack->right!=NULL){if(abs(stack->height-stack->height)<=1)state=0;else{state=-1;stack_clear();}}}stack_clear();return(state);}//建立remove_tree函式int remove_tree(tree_node_t *tree){travel(tree);if(stack_empty())return(-1);else{while(!stack_empty()){return_node(pop());}return(0);}}void main(){tree_node_t *atree=NULL;obj_node_t obj[256],*f; //MAXSIZE=n(number of leaf)+(n-1) number of nodeint n,j=0;cout<<"Now Let's start this program! There is no tree in memory.\n";int item;while(item!=0){cout<<"\nRoot address = "<<atree<<"\n";cout<<"\n1.Create a tree\n";cout<<"\n2.Insert a int type object\n";cout<<"\n3.Test the structure of the tree\n";cout<<"\n4.Find a object\n";cout<<"\n6.Delete a object\n";cout<<"\n7.Remove the Tree\n";cout<<"\n0.Exit\n";cout<<"\nPlease select:";cin>>item;cout<<"\n\n\n";switch(item){case 1:{atree=creat_tree();cout<<"\nA new empty tree has been built up!\n";break;}case 2:{if(atree!=NULL)while(n!=3458){cout<<"Please insert a new object.\nOnly one object every time(3458 is an end code) : ";cin>>n;if(n!=3458){obj[j].obj_key=n;if(insert(atree,&obj[j])==0){j++;cout<<"Integer "<<n<<" has been input!\n\n";}elsecout<<"\n\nInsert failed!\n\n";}}elsecout<<"\n\nNo tree in memory,insert Fail!\n\n";break;}case 3:{if(atree!=NULL){n=test_structure(atree);if(n==-1)cout<<"\n\nIt's not a correct AVL tree.\n\n";if(n==0)cout<<"\n\nIt's a AVL tree\n\n";}elsecout<<"\n\nNo tree in memory,Test Fail!\n\n";break;}case 4:{if(atree!=NULL){cout<<"\n\nWhat do you want to find? : ";cin>>n;f=find(atree,n);if(f==NULL){cout<<"\n\nSorry,"<<n<<" can't be found!\n\n";}else{cout<<"\n\nObject "<<f->obj_key<<" has been found!\n\n";}}elsecout<<"\n\nNo tree in memory,Find Fail!\n\n";break;}case 5:{if(atree!=NULL){travel(atree);for(int count=0;count<i;count++){cout<<" "<<stack[count]->key<<",";}}elsecout<<"\n\nNo tree in memory,Travel Fail!\n\n";break;}case 6:{if(atree!=NULL){cout<<"\n\nWhich object do you want to delete?\n\n";cin>>n;if(del(atree,n)==0){cout<<"\n\n"<<n<<" has been deleted!\n\n";}elsecout<<"\n\nNo this object\n\n";}elsecout<<"\n\nNo tree in memory,Delete Fail!\n\n";break;}case 7:{if(atree!=NULL){remove_tree(atree);cout<<"\n\nThe Tree has been removed!\n\n";atree=NULL;}elsecout<<"\n\nNo tree in memory,Removing Fail!\n\n";}default:cout<<"\n\nNo this operation!\n\n";}n=0;}}