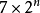142857，又名走馬燈數。它發現於埃及金字塔內，它是一組神奇的數字，它證明一星期有7天，它自我累加一次，就由它的6個數字，依順序輪值一次，到了第7天，它們就放假，由999999去代班，數字越加越大，每超過一星期輪迴，每個數字需要分身一次，你不需要計算機，只要知道它的分身方法，就可以知道繼續累加的答案，它還有更神奇的地方等待你去發掘！
基本介紹
- 中文名：142857
- 別名：走馬燈數
- 發現：發現於埃及金字塔內
- 美譽：世界上最神奇的數字
- 拆分：單數和都是“9”
規律,神奇的解答,累加輪轉,其他研究,
規律
世界上最神奇的數字是：142857
（142857=3×3×3×11×13×37）
看似平凡的數字，為什麼說它最神奇呢？
我們把它從1乘到10看看
142857 × 1 = 142857 1*7=7
142857 × 2 = 285714 2*7=14
142857 × 3 = 428571 3*7=21
142857 × 4 = 571428 4*7=28
142857 × 5 = 714285 5*7=35
142857 × 6 = 857142 6*7=42
142857 × 7 = 999999 7*7=49
142857 × 8 = 1142856 8*7=56
142857 × 9 = 1285713 9*7=63
142857 × 10 = 1428570 10*7=70
規律：1-6同樣的數字，只是調換了位置，反覆的出現。
1-6的結果，橫豎都有（142857）沒有0369 神奇吧。有點像“數獨”不過是沒有0369的數獨。
乘以7我們會驚人的發現是999999,9+9+9+9+9+9=54（5+4=9）
而142 + 857 = 999 14 + 28 + 57 = 99 1+4+2+8+5+7=27（2+7=9）
最後，我們用142857乘以142857答案是：20408122449
20408122449的前五位+上後六位的得數是多少呢？
20408 + 122449 = 142857
那么把它繼續乘下去會發生什麼呢？
142857 × 8 = 1142856 1+142856= 142857
142857 × 9 = 12857131+285713= 285714
142857 ×10= 1428570 1+428570= 428571
142857 ×11= 1571427 1+571427= 571428
142857 ×12= 1714284 1+714284=714285
142857 ×13= 1857141 1+857141=857142
142857 ×14= 19999981+999998= 999999
142857 ×15= 2142855 2+142855= 142857
142857 ×16= 2285712 2+285712= 285714
142857 ×17=2428569 2+428569= 428571
..............
我們發現，其實142857不管乘以幾所得出來的數前後相加總能得到由1.4.2.8.5.7這幾個數按一定的順序組成的數字。
再來看看除法：
142857 ÷7= 20408.142857142857142857142857....
285714 ÷7= 40816.285714285714285714285714285714..
428571 ÷7= 61224.428571428571428571428571428571..
571428 ÷7= 81632.571428571428571428571428....
714285 ÷7=102040.714285714285714285714285...
857142 ÷7=122448.857142857142857142...
1÷7=0.142857142857...
2÷7=0.2857142857142857...
3÷7=0.42857142857142857...
4÷7=0.57142857142857...
5÷7=0.7142857142857...
6÷7=0.857142857142857...
142857÷2=71428.5
142857÷5=28571.4
857×857=734449 142×142=20164
734449-20164=714285
還有142857乘以含7的任意數字，算出來的結果的各個數字之和等於36（除77、147、217、287、357......被7整除的外和107、177、207、247、277、307、317、347、377、387......等數值），如：
142857×17=2428569 2+4+2+8+5+6+9=36
142857×27=3857139 3+8+5+7+1+3+9=36
142857×37=5285709 5+2+8+5+7+0+9=36
142857×47=6714279 6+7+1+4+2+7+9=36
......
神奇的解答
142857×1=142857（原數字）
142857×2=285714（輪值）
142857×3=428571（輪值）
142857×4=571428（輪值）
142857×5=714285（輪值）
142857×6=857142（輪值）
142857×7=999999（放假由9代班）
7×（1~6）的積的個位排在末尾 7×7=49，積是6個9
142857×8=1142856（7分身，即分為頭一個數字1與尾數6，數列內少了7）
142857×9=1285713（4分身）
142857×10=1428570（1分身）
142857×11=1571427（8分身）
142857×12=1714284（5分身）
142857×13=1857141（2分身）
142857×14=1999998（9也需要分身變大）
7×（8~14）的個位的積的個位+1就是需要變化的數
以上各數的單數和都是“9”。有可能藏著一個大秘密喔!
繼續算下去……
142857除以7小數部分可以得到142857142857142857142857無限循環小數
把142857拆成14+28 +57 =99 ; 142+857=999; 1+4+2+8+5+7=27，2+7=9；您瞧瞧，它們的單數和竟然都是“9”。依此類推，上面各個神秘數，它們的單數和都是“9”(如142857可以挑出三段寫成1+8 4+5 2+7 這都等於9)且它的雙數和為27還是3的三次方.
而把142857拆成如 1+4+2+8+5+7 或 14+2+85+7 或 14285+7等等任意的組合（相鄰數字隨意組合） 所得結果都是9的倍數。
而當乘數超過了7*9=63時(如64)單數和不再是27(3*9)而是36(4*9).142857的分身規律到了這裡就不復存在了. 直到142857*(7*14)=100999899才恢復了規律. [附:142857*7*14=13999986 單數和為54(6*9)]很明顯在這裡出現了規律的"斷層"但至此以後這種"斷層"將不會出現。]
那142857是怎么來的呢，我們在繼續計算：
9÷7=1.2857142857142857142857142857......
99÷7=14.142857142857142857142857142857......
999÷7=142.7142857142857142857142857......
9999÷7=1428.42857142857142857142857142857......
99999÷7=14285.57142857142857142857142857......
999999÷7=142857
好了，142857整數出現了，那我們繼續......
9999999÷7=1428571.2857142857142857142857142857......
99999999÷7=14285714.142857142857142857142857......
999999999÷7=142857142.7142857142857142857142857......
9999999999÷7=1428571428.42857142857142857142857142857......
99999999999÷7=14285714285.57142857142857142857142857......
999999999999÷7=142857142857 (12個9，和6個9一樣得到的是整數）
9999999999999÷7=1428571428571.2857142857142857142857142857......
13個9，小數點後的數字和9÷7相同）
99999999999999÷7=14285714285714.142857142857142857142857......
14個9，小數點後的數字和999÷7相同）
.
.
.
.
如此循環，18個9除以7等於多少呢？等於142857142857142857——三組“142857”，24個9除以7呢？是142857142857142857142857——四組“142857”.......
還有呢：
1÷7=0.14285714285714285
2÷7=0.2857142857142857
3÷7=0.42857142857142854
4÷7=0.5714285714285714
5÷7=0.7142857142857143
6÷7=0.8571428571428571
8÷7=1.1428571428571428
……
……
……
14÷7=2
28÷7=4
57÷7=8.142857142857.......
142857×142857 = 20408122449，20408+122449=142857
20408122449×2 = 40816244898， 40816+244898=285714=142857×2
20408122449×3 = 61224367347， 61224+367347=428571=142857×3
20408122449×4 = 81632489796， 81632+489796=571428=142857×4
20408122449×5 = 102040612245， 102040+612245=714285=142857×5
20408122449×6 = 122448734694， 122448+734694=857142=142857×6
20408122449×7 = 142856857143， 142856+857143=999999=142857×7
20408122449×8 = 163264979592， 163264+979592=1142856，1+142856=142857
20408122449×9 = 183673102041， 183673+102041=285714=142857×2
20408122449×10 = 204081224490， 204081+224490=428571=142857×3
20408122449×11 = 224489346939， 224489+346939=571428=142857×4
..... 後面還有
而這個數是如何得來的呢，大家可以試一下，只要用1除以7就可以發現0.142857142857142857……
前面說到的142857，其實根本不神奇。
你看:1÷7=0.142857142857142857142857.....
至於142857×7=999999，實際上，1/7×7≈0.142857……*7=0.999999.....他們之間的關係不言而喻。
能被7整除的自然數的個數
10以內 1個
100以內 14個
1000以內 142個
10000以內 1428個
100000以內 14285個
1000000以內 142857個
10000000以內 1428571個
......
100以內 14個
1000以內 142個
10000以內 1428個
100000以內 14285個
1000000以內 142857個
10000000以內 1428571個
......
數字的拆分
142857142857142857142857拆分。
7×2=14
14×2=28
28×2=56
56×2=112
112×2=224
224×2=448
448×2=896
896×2=1792
1792×2=3584
3584×2=7168
7168×2=14336
這樣的一組數字。暫時得到這樣的數字。
這樣排列他們
1 | 4 | 2 | 8 | 5 | 7 | 1 | 4 | 2 | 8 | 5 | 7 | 1 | 4 | 2 | 8 | 5 | 7 | 1 | 4 |
1 | 4 | ||||||||||||||||||
2 | 8 | ||||||||||||||||||
5 | 6 | ||||||||||||||||||
1 | 1 | 2 | |||||||||||||||||
2 | 2 | 4 | |||||||||||||||||
4 | 4 | 8 | |||||||||||||||||
8 | 9 | 6 | |||||||||||||||||
1 | 7 | 9 | 2 | ||||||||||||||||
3 | 5 | 8 | 4 | ||||||||||||||||
7 | 1 | 6 | 8 | ||||||||||||||||
1 | 4 | 3 |
這個數字表格顯示出來，發現142857這個數字循環可以用某種2n次方的數字乘以7的組合加成獲得。
142857×7=999999
142857證明
這些數以
的序列排列並除以
得
，即
.
累加輪轉
142857自我累加
142857+142857=285714
285714+142857=428571
428571+142857=571428
571428+142857=714285
714285+142857=857142
等式右邊均為142857數字的輪轉。
②再加翻車
857142+142857=999999
③拆和翻車
把上邊6個數分別拆解求和
142+857=999
285+714=999
428+571=999
571+428=999
714+285=999
857+142=999
④平方拆和
換一種方式，先平方，再拆解求和平方拆分後再加起來，又回到了142857的倍數。
原理
輪轉原理
把逐次乘10，則小數點逐次右移：
兩邊取小於1的部分，得：
其中 ri為 10模7的余。
由於循環節長為6，所以中間6個數互不相等，且小數前6位由142857輪轉得到。與右邊算式的小數前6位比較：左邊代表輪轉數，右邊代表累加數，於是得到輪轉原理。（右邊算式中，省略部分乘ri不會進1。）
循環節恰好為m-1，在這裡起了關鍵作用。
142857性質總表
- 走馬
- 輪值（1-7）
- 代班（8-14）
- 9原理
- 平方原理
- 數字組合
- 累加輪轉
（1）自我累加
（2）再加翻車
（3）拆和翻車
（3）平方拆和
其他研究
經過研究發現，並不僅僅7存在這樣的神奇效果：
