龐加萊一萊特希爾一郭法(Poincare-Lighthill-Kuo method)簡稱PLK法一種偏微分方程數值解法.指用漸近展開法求解非線性數理問題出現高階奇性增強的困難時,把自變數加以適當變形並作展開的一種求解方法。以下用一階常微分方程模型問題的分析來說明萊特希爾(Lighthill , M. J.)改進的變形坐標法
因此,當e+l}u(0)}雖很大,但有限.分析直接展開解不能一致有效的原因在於方程在直線二+eu = 0上有奇性;然而線性近似uo(二)=1/二卻將奇性轉移到二=0處,這種偏離了的奇性在高階項中變得更強.運用非線性的變形坐標法可以消除高階奇性,即把自變數二用非線性變換變到濘,而u也變為寧的}I,即作下而的展開
基本介紹
- 中文名:龐加萊一萊特希爾一郭法
- 別名:PLK法
- 分類:微分方程
- 作者 :龐加萊
- ISBN:7544024008
龐加萊一萊特希爾一郭法(Poincare-Lighthill-Kuo method)簡稱PLK法一種偏微分方程數值解法.指用漸近展開法求解非線性數理問題出現高階奇性增強的困難時,把自變數加以適當變形並作展開的一種求解方法。以下用一階常微分方程模型問題的分析來說明萊特希爾(Lighthill , M. J.)改進的變形坐標法

龐加萊一萊特希爾一郭法
因此,當e+l}u(0)}雖很大,但有限.分析直接展開解不能一致有效的原因在於方程在直線二+eu = 0上有奇性;然而線性近似uo(二)=1/二卻將奇性轉移到二=0處,這種偏離了的奇性在高階項中變得更強.運用非線性的變形坐標法可以消除高階奇性,即把自變數二用非線性變換變到濘,而u也變為寧的}I,即作下而的展開

龐加萊一萊特希爾一郭法
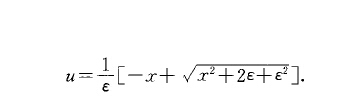
龐加萊一萊特希爾一郭法
這正是問題的精確解。
PLK法的突出優點是簡單靈活,通常只需求得
零階或一階解,即可達到相當高的準確度.PLK法
在用於雙曲型方程時一般不會發生困難,但用於橢圓型或拋物型方程時,有時可能失效.
PLK法是由林斯泰特(Lindstidt , A.)於1882年和龐加萊(Poincare , ( J. -) H.)等人於1886年始創.他們在尋求非線性常微分方程組的周期解時,為了消除長期項,把問題中的頻率參數加以變形,這相當於將自變數(坐標)作線性變換而收到成效.因此林斯泰特一龐加萊法也稱“變形坐標法”.使用上述方法在求解某些問題的高階近似時可能出現強奇性,萊特希爾(Lighthill , M. J.)於1949年進一步引進了自變數的非線性變換,求得了一系列物理問題的一致有效漸近解。中國學者郭永懷於1953年,1956年把變形坐標法和邊界層方法結合起來,解決了大雷諾數粘性流動和超聲速邊界層等難題.為此,錢學森於1956年撰文總結了上述方法,並命名為龐加萊一萊特希爾一郭法,其中的郭(Kuo)指郭永懷.
PLK法(PLK method)即“龐加萊一萊特希爾-郭法”.
