龍貝格求積公式也稱為逐次分半加速法。是數值計算方法之一,用以求解數值積分。是在梯形公式、辛普森公式和柯特斯公式之間關係的基礎上,構造出一種加速計算積分的方法。 作為一種外推算法,在不增加計算量的前提下提高了誤差的精度。
基本介紹
- 中文名:龍貝格求積公式
- 外文名:Romberg quadrature formula
- 類別:數值計算方法之一
- 作用:用以求解數值積分
- 別名:逐次分半加速法
- 套用學科:數學術語
概述
推導過程


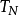
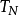

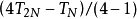


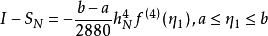
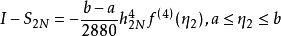

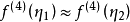







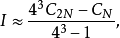






龍貝格求積公式也稱為逐次分半加速法。是數值計算方法之一,用以求解數值積分。是在梯形公式、辛普森公式和柯特斯公式之間關係的基礎上,構造出一種加速計算積分的方法。 作為一種外推算法,在不增加計算量的前提下提高了誤差的精度。


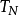
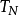

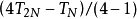


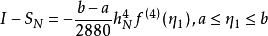
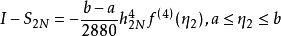

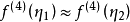



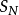
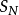




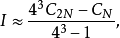





龍貝格求積公式也稱為逐次分半加速法。是數值計算方法之一,用以求解數值積分。是在梯形公式、辛普森公式和柯特斯公式之間關係的基礎上,構造出一種加速計算積分的...
構造數值積分公式最通常的方法是用積分區間上的n 次插值多項式代替被積函式,由此...使用方便、穩定性好等優點,因此在等距情形宜採用龍貝格求積公式(Rhomberg ...
6.4龍貝格求積1846.4.1外推算法1846.4.2梯形加速公式1856.4.3辛普生加速公式1886.4.4龍貝格求積的一般公式1896.4.5龍貝格求積的算法和程式190...
5.4 龍貝格求積公式 5.5 高斯公式 5.6 數值微分 習題 6 解線性方程組的直接法 6.1 引言 6.2 高斯消去法 6.3 向量和矩陣的範數 6.4 矩陣的條件...
8.3.3復化科特斯求積公式8.4龍貝格積分方法8.4.1後驗誤差估計8.4.2變步長梯形公式8.4.3理查森外推法8.4.4龍貝格算法8.5高斯求積公式...
8.4 外推算法與龍貝格算法 2128.4.1 變步長的求積公式 2128.4.2 外推算法 2148.4.3 龍貝格求積公式 2148.5 高斯求積公式 2188.5.1 高斯點與高斯求積公式 218...
4.4 龍貝格求積公式 4.5 高斯求積公式 習題4 第5章 線性方程組的解法 5.1 預備知識 5.2 高斯消元法 5.3 直接三角分解法 5.4 疊代法的一般理論 ...
公式的近似值進行加權平均獲得準確程度較高的積分近似值的一種方法,它具有公式簡練、計算結果準確、使用方便、穩定性好等優點,因此在等距情形宜採用龍貝格求積公式。...
3.3.2 復化辛普森公式 923.4 龍貝格求積公式 943.4.1 梯形法的遞推化 943.4.2 龍貝格算法 963.5 高斯求積公式 973.6 數值微分 101...
6.3.3 龍貝格加速公式的MATLAB程式6.4 高斯型求積公式及其MATLAB實現6.4.1 高斯型求積公式6.4.2 高斯公式的MATLAB程式6.5 數值微分法...
7.3龍貝格求積法7.4高斯求積法7.4.1代數精度的概念7.4.2高斯求積法7.4.3幾種常用的高斯求積公式7.5高振盪函式求積法7.6數值微分...
4.4復化求積公式 4.5龍貝格求積公式 4.6高斯求積公式 4.7數值微分 小結4 習題4 第5章線性方程組的直接解法 5.1問題的提出 5.2高斯消去法 5.3矩...
4.2.3 辛普森公式的餘項(105) 4.3 複合求積公式(106) 4.3.1 複合梯形公式(106) 4.3.2 複合辛普森求積公式(107) 4.4 龍貝格求積公式(109) 4.4.1 梯形法的遞...
7.6龍貝格求積公式7.7MATLAB的套用習題7第8章常微分方程的數值解法8.1歐拉方法8.1.1向前歐拉方法8.1.2歐拉方法的誤差分析8.1.3向後歐拉方法...
6.3.2龍貝格求積法 6.4高d斯求積公式 6.4.1高斯求積公式的基本理論 6.4.2常用高斯求積公式 6.4.3高斯求積公式的餘項與穩定性 6.5數值微分 6.5.1插值型求導公...
7.4.2龍貝格積分法7.5高斯求積公式7.6數值微分7.6.1兩點公式7.6.2三點公式7.6.3五點公式習題第8章矩陣的特徵值與特徵向量的計算...
4.3牛頓 柯特斯求積公式4.4復化求積公式4.5龍貝格求積公式4.6高斯求積公式4.7數值微分第5章線性方程組的直接解法5.1問題的提出5.2高斯消去法...
6.3.2 龍貝格求積法6.4 高d斯求積公式6.4.1 高斯求積公式的基本理論6.4.2 常用高斯求積公式6.4.3 高斯求積公式的餘項與穩定性6.5 數值微分...
3.4.2龍貝格算法 3.5高斯求積公式 3.6數值微分 3.7數字圖像的導數與梯度 3.7.1二維數據的一階導數 3.7.2二維數據的二階導數 習題 第4章解線性方...
第8章 數值積分8.1 辛普生求積公式8.2 龍貝格積分法8.3 二重積分8.4 主值積分8.5 積分轉化為有限項求和第9章 本徵問題9.1 乘冪法9.2 雅可比方法...
5.4.2龍貝格求積公式5.5高斯型求積公式5.5.1定義及性質5.5.2常用高斯型求積公式5.6數值微分5.6.1差商代替微商5.6.2插值型數值微分公式...
8.3 復化求積公式 8.3.1 復化梯形求積公式及其餘項 8.3.2 復化辛普森求積公式及其餘項 8.3.3 區間逐次分半求積法 8.4 龍貝格求積方法 8.5 高斯求積公式 8.5....
