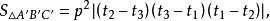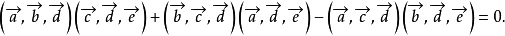基本介紹
- 中文名:默比烏斯定理
- 外文名:Möbius theorem
- 別名:麥比烏斯定理
- 所屬學科:數學
- 所屬問題:高等幾何(射影幾何)
基本介紹,兩圓的麥比烏斯定理,拋物線的麥比烏斯定理,
基本介紹
默比烏斯定理 設A、B、C、D、E、F為空間的六個點,(ABDF)表示由 為棱組成的平行六面體的有向面積(其他仿此),則
為棱組成的平行六面體的有向面積(其他仿此),則

(ABDF)(CDEF)+(BCDF)(ADEF)+(CADF)(BDEF)=0.
該定理是麥比烏斯於1827年得到的。
取F為原點,設 ,則據雙重向量積有
,則據雙重向量積有


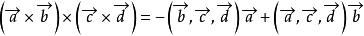
於是得 和
和

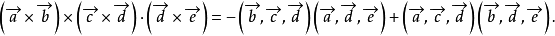

即
又 ,
,

所以

兩圓的麥比烏斯定理
通過兩圓的交點A分別作兩條直線PQ和P'Q',分別與圓相交於P、P'和Q、Q' ,則PP'與QQ'的交角∠S的大小一定。
 圖1
圖1該定理是德國數學家麥比烏斯於1837年得到的。設兩圓的另一個交點為B,連結AB、P'B、BQ',因為兩圓中的AB弧確定,所以∠Q'P'B和∠P'Q'B大小一定,從而∠P'BQ'的大小也一定,又因為∠SPQ=∠P'BA,∠ABQ' =∠Q,所以∠SPQ+∠SQP=∠P'BA+∠ABQ' =∠P'BQ'為定值,因此,PP'與QQ'的交角∠S的大小一定。
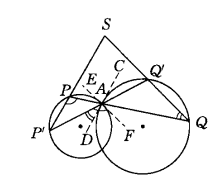 圖2
圖2如果過A點分別作兩圓的切線CD、EF,則∠CAQ'=∠Q,∠P'PA =∠P'AF,所以∠S =∠P'PA一∠Q =∠P'AF-∠Q。但∠CAQ' =∠P'AD,故∠S=∠P'AF-∠P'AD= ∠DAF。由於∠DAF是兩圓的交角,它的大小是一定的。所以∠S的大小也一定。應當注意,這裡只是給出了一種情形,還有多種情形的圖存在。
 圖3
圖3拋物線的麥比烏斯定理
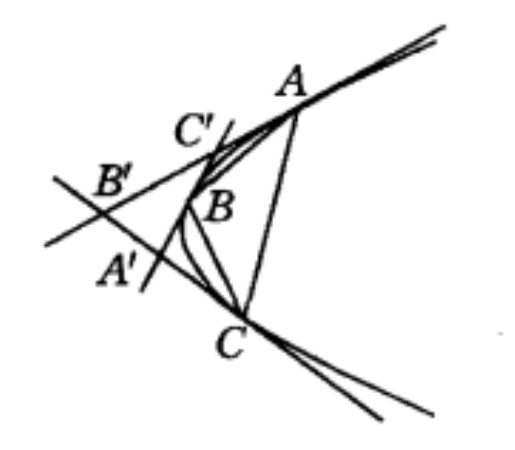
分別過拋物線內接三角形ABC的頂點作切線,設它們各交於A'、B'、C',則

該定理是麥比烏斯於1827年得到的。
設拋物線的方程為
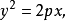
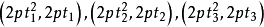
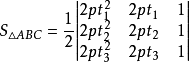

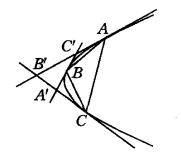 圖4
圖4分別過A、B、C的該拋物銭的切線方程為

由(1)與(2)聯立,解得 ,所以點A'的坐標為
,所以點A'的坐標為 ,同祥可得B'、C'的坐標各為
,同祥可得B'、C'的坐標各為


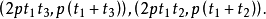
所以 的絕對值,通過計算得
的絕對值,通過計算得