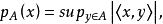麥基拓撲

設(X,Y)為對偶線性空間，在Y的每個弱緊凸集上一致收斂的拓撲是一種可允許拓撲，稱為X上的麥基拓撲。

基本介紹

• 中文名：麥基拓撲
• 外文名：Mackey topology
• 適用範圍：數理科學

簡介

設(X,Y)為對偶線性空間，在Y的每個弱緊凸集上一致收斂的拓撲是一種可允許拓撲，稱為X上的麥基拓撲，記為τ(X,Y)。

性質

X上一個局部凸拓撲成為相容拓撲的充分必要條件是它比弱拓撲σ(X,Y)強，而比τ(X,Y)弱。

麥基拓撲是最強的相容拓撲。

原來的拓撲與麥基拓撲τ(E,E′)相同的局部凸空間E稱為麥基空間。擬桶型空間是麥基空間。

可允許拓撲

可允許拓撲是一種局部凸拓撲。

設(X,Y)是對偶線性空間，𝒴是Y中的有界集族，且並U{A|A∈𝒴}的線性包是Y，即Y是U{A|A∈𝒴}張成的線性空間，對每個A∈𝒴，定義半範數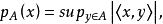

則由半範數族{p_A(x)|A∈𝒴}確定的X上局部凸拓撲T_𝒴，稱為關於對偶線性空間(X,Y)的一個可允許拓撲，或在集類𝒴上的一致收斂拓撲，而相應的有界集族𝒴稱為可允許集族。