馬丟函式

馬丟函式是馬丟方程的周期基本解

基本介紹

• 中文名：馬丟函式
• 實質：馬丟方程的周期基本解
• 所屬：馬丟方程
• 學科：數學

正弦函式

馬丟正弦函式 有如下性質

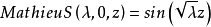
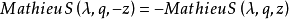
餘弦函式

馬丟餘弦函式有如下性質：

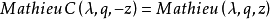
另

周期性

馬丟函式 MathieuC(a,q,z) 或 MathieuS(a,q,z) 只有一個是周期為 <math>\pi</math> 或<math>2\pi</math>的周期解，另一個不是。

馬丟函式 MathieuC(a,q,z) 和 MathieuS(a,q,z) 兩者都有是周期為<math>2n\pi</math>（n≥2)的周期函式。

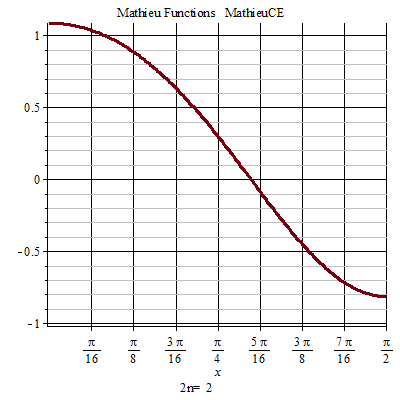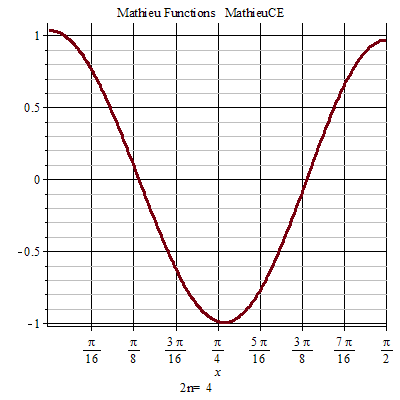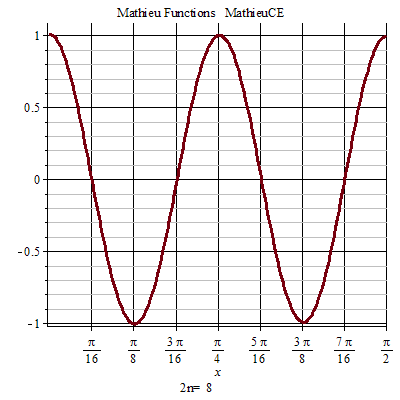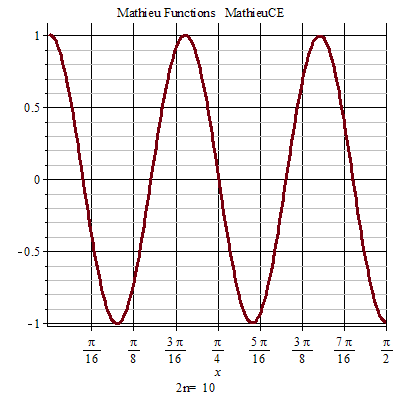馬丟函式周期性

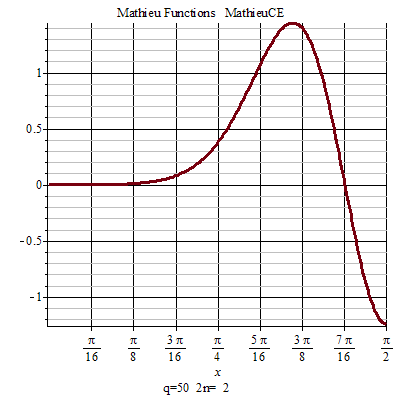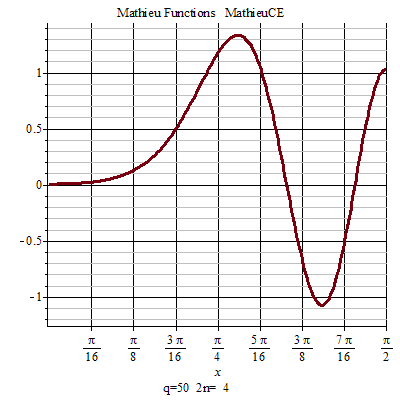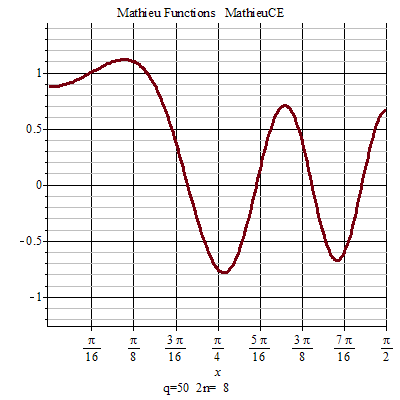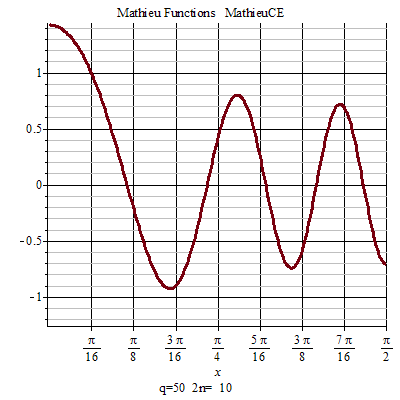馬丟函式周期性

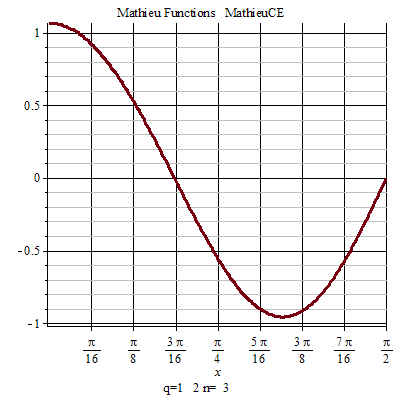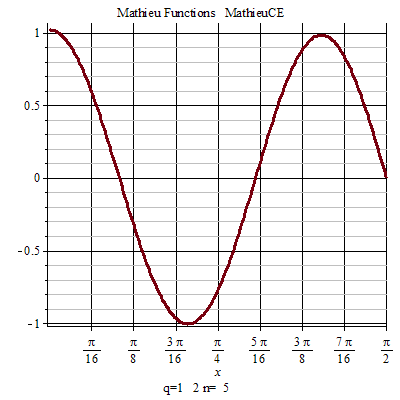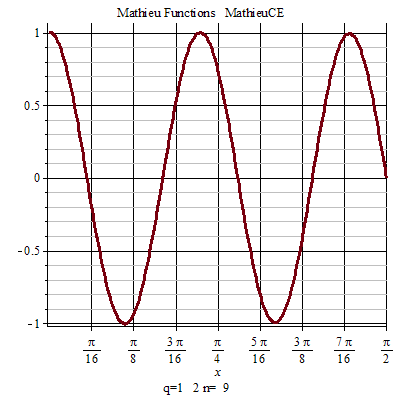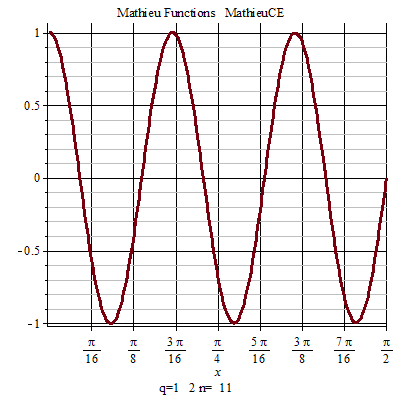馬丟函式周期性

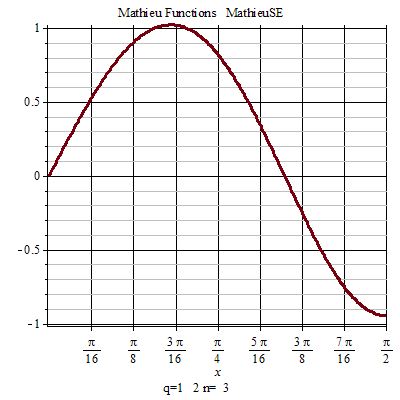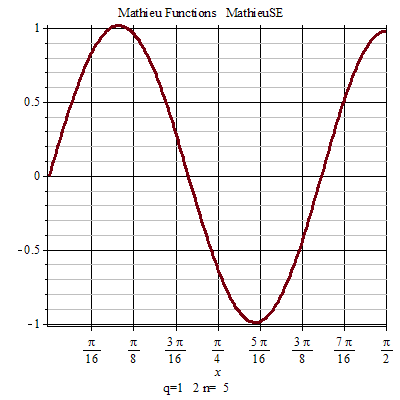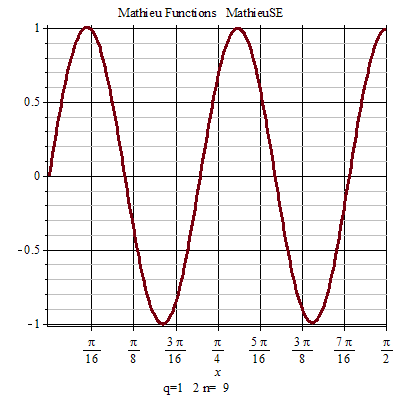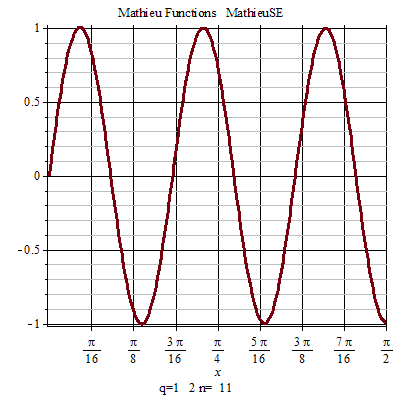馬丟函式周期性

正交性

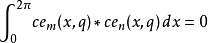
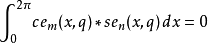
特徵方程

馬丟方程的特徵方程是<ref name=W>605頁</ref>

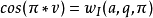
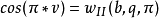
對於給定的v，q, 上列特徵方程給出無窮多個a、b解稱為特徵值。

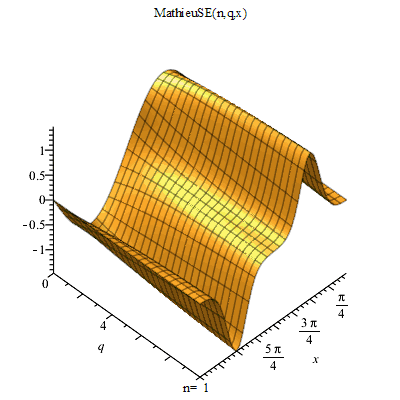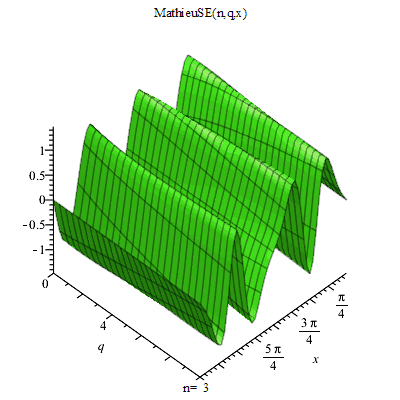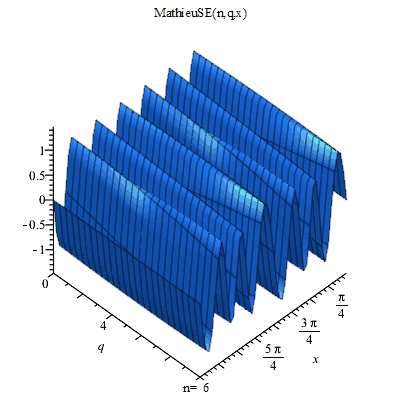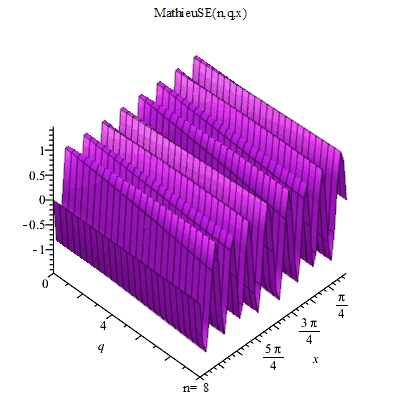馬丟函式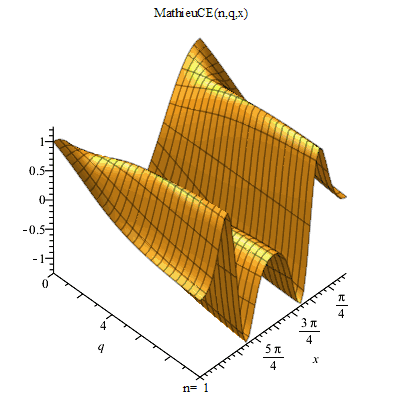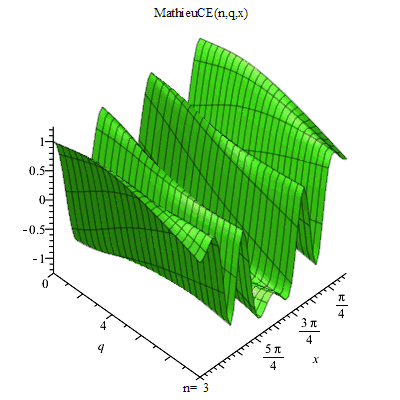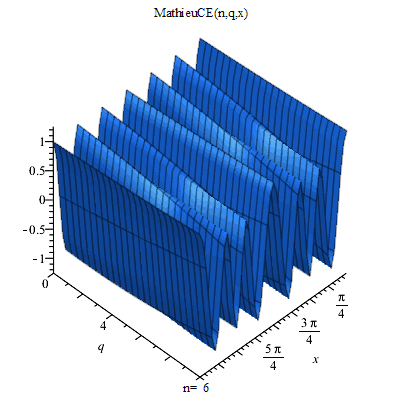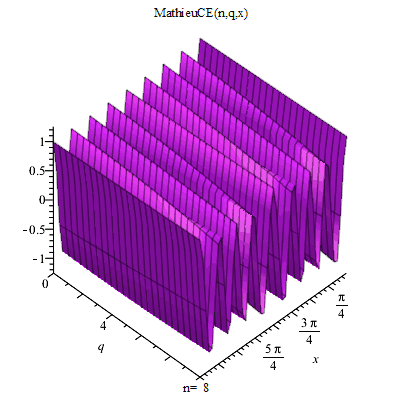

馬丟函式周C

馬丟函式體特徵值可展開成級數：<ref name=FRa>Frank p659</ref>

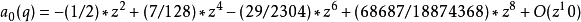
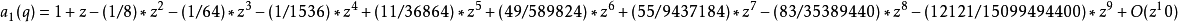
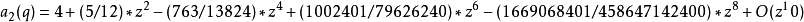
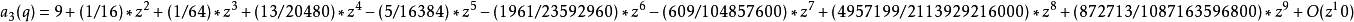
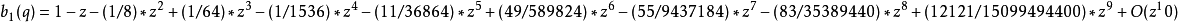
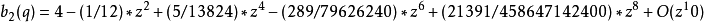
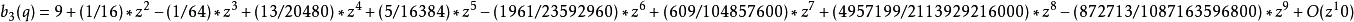
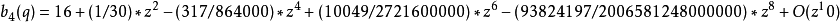
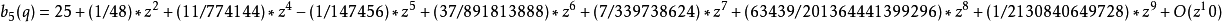
馬丟正弦函式

馬丟餘弦函式