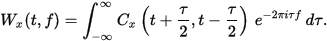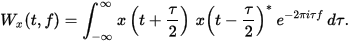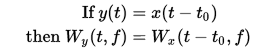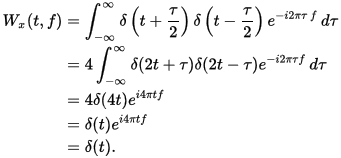韋格納分布

韋格納分布是由1963年的諾貝爾物理學獎得主尤金·保羅·韋格納，於1932年首次引用了一個新的方程式。韋格納分布是一種重要的雙線性時頻分布，具有解析度高、能量集中和滿足時頻邊緣特性等優良特性。也被音譯為“維格納分布”。但該時頻分布是雙線性的，對於多分量信號而言，韋格納分布存在嚴重的交叉項干擾。

基本介紹

• 中文名：韋格納分布
• 外文名： wigner quasiprobability distribution
• 分類：計算機 數學
• 缺點 ：交叉項干擾
• 提出者：尤金·保羅·韋格納
• 又名：維格納分布

數學定義

韋格納分布函式有幾個不同的定義。這裡給出的定義特定於時頻分析。給定時間序列x [t]，其非穩態自相關函式由下式給出

然後通過以平均時間表示自相關函式給出t=(t1+t2)/2和時間滯後 =t1-t2，傅立葉變換滯後。

因此，對於單個（平均零）時間序列，韋格納分布函式簡單地是

韋格納分布函式的功能是隨時降低光譜密度函式t，對於固定過程，完全等同於非平穩自相關函式。因此，韋格納分布函式告訴我們（大概）頻譜密度如何隨時間變化。

交叉項干擾

韋格納分布函式不是線性變換。當輸入信號中存在多於一個分量時，會發生交叉項（“時間跳動”），與頻率跳動相似。該時頻分布是雙線性的，對於多分量信號而言，韋格納分布存在嚴重的交叉項干擾。相比之下，短時傅立葉變換沒有這個特徵。韋格納分布的負特徵反映了經典信號的伽柏極限，與物理上與量子結構的任何可能的底層無關。

以下是展示韋格納分布函式的交叉干擾的一些示例。

為了減少交叉干擾，已經提出了其他幾個變換，包括修改的韋格納分布函式，伽柏-韋格納變換和科恩類分布。

性質

韋格納分布函式具有下面列出的幾個明顯屬性。

投影屬性

恢復屬性

時刻屬性

區域屬性

乘法定理

卷積定理

時變協方差

時間-頻率分析示例

以下是一些示例，說明如何在時間 - 頻率分析中使用韋格納分布。

恆定輸入信號

當輸入信號恆定時，其時間 - 頻率分布是沿著時間軸的水平線。例如，如果x（t）= 1，那么

當輸入信號為正弦函式時，其時頻分布是與時間軸平行的水平線，由正弦信號的頻率偏移。

德爾塔輸入信號

當輸入信號為增量函式時，由於在t = 0時它只是非零，並且包含無窮大的頻率分量，所以它的時間 - 頻率分布應該是跨原點的垂直線。這意味著delta函式的時間頻率分布也應該是delta函式。由韋格納分布可知

當輸入信號的相位為二階或更低時，Wigner分布函式最適合於時間 - 頻率分析。對於這些信號，韋格納分布可以精確地產生輸入信號的時間頻率分布。

優缺點

優點：

1.有良好的解析度，尤其是對單一成分，且瞬時頻率變化不為2次式以上。

2.有好的數學運算性質。

3.可用於分析隨機程式。

缺點：

1.有相交項(cross term)的問題。

2.需要更多的時間去計算，若訊號時間越長，則需要更久的時間。

3.不是一對一函式，無法辨別相位部分。

4.不適合分析瞬時頻率變化為2次式以上的型態。