鞅差序列 (martingale-differencesequence)與鞅差概念相關。當期望值服從於過往值都為零的假設時,一個隨機序列X是一個鞅差序列(MDS)。鞅差序列 (martingale-differencesequence)是一類隨機序列。指部分和序列是鞅的隨機序列。
基本介紹
- 中文名:鞅差序列
- 外文名:martingale-differencesequence
- 領域:數學
- 性質:一類隨機序列
- 定義:部分和序列是鞅
- 空間:機率空間
概念,鞅,鞅差,隨機過程,
概念
鞅差序列 (martingale-differencesequence)是一類隨機序列。指部分和序列是鞅的隨機序列。設X={X(n),n≥0}是定義在機率空間(Ω,F,P)上的隨機序列。{Fn}n≥0是一上升σ代數族。稱X為鞅差序列,如果下列條件成立:
1.X是{Fn}適應,即對每一n≥0,X(n)是Fn可測的。
2.對每一n≥0,X(n)是可積的。
3.對每一n≥0,E[X(n+1)|Fn]=0 a.s.P。
如果Y={Y(n),n≥0}是一{Fn}鞅,則由X(0)=Y(0),X(n)=Y(n+1)-Y(n)(對n≥1)定義的序列X={X(n),n≥0}是關於{Fn}的鞅差序列。反之,若X={X(n),n≥0}是關於上升σ代數族{Fn}n≥0的鞅差序列,則由:
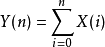
鞅
鞅是一類重要的隨機過程。設{X(t),t∈R+}是定義在機率空間(Ω,F,P)上適應於上升σ代數族{Ft}t∈R+的隨機過程.稱{X(t),t∈R+}為{Ft}鞅,如果下列兩條件成立:
1.對每一t∈R+,X(t)可積。
2.對任意t>s≥0,E[X(t)|Fs]=X(s) a.s.p。
由條件2立即推出E[X(t)]=E[X(s)]。martingale一詞意指一種馬具,即中文的“鞅”,但亦指西方賭博中的一種輸後加倍下注的賭法。
在離散時間情形,鞅有如下直觀意義:設X(0)表示賭徒開始參加賭博時的賭本,X(n)(n≥1)表示他在第n局賭博後的總賭金(即賭本X(0)與前n局的輸贏之總和),而Fn=σ(X(i), i=0,1,…,n),反映了前n局賭博的全部信息.如果{X(n),n≥0}是關於{Fn}n≥0的鞅,則條件E[X(n+k)|Fn]=X(n)表示在已知前n局輸贏的條件下,再經過k局(k≥1)賭博後,賭徒的總賭金在平均意義下是和他在第n局後的總賭金相等的。這就是說賭博是“公平的”。對於這種賭博,不管用什麼賭法,按平均來說,賭徒最終不會從賭博中得益或輸蝕。
鞅差
設X={Xt,t≥0}為一隨機過程,E(Xt|Xu,u≤s)表示 Xt關於{Xu,u≤s}的條件期望。若對任意的s≤t,E(Xt| Xu,u≤s)=0以機率1成立,則稱X={Xt,t≥0}為鞅差。 若X={Xn,n∈N}為鞅,Yn=Xn-Xn-1,n≥1,X0=Y0,則 Y={Yn,n ∈N}為鞅差序列。反之,若Y={Yn,n ∈N}為鞅差序列,Xn=Yj,則X={Xn,n ∈N}為鞅。
隨機過程
隨機過程是隨時間推進的隨機現象的數學抽象。設(Ω,ℱ,P)為機率空間,T為指標t的集合,如果對每個t∈T,有定義在Ω上的實隨機變數X(t)與之對應,就稱隨機變數族X={X(t),t∈T}為一隨機過程。
人們對一些特殊的隨機過程早有研究。1907年前後,俄國數學家馬爾可夫提出並研究一種能用數學分析方法研究自然過程的一般圖式,後人稱這種圖式為馬爾可夫鏈。1923年,美國數學家N.維納從數學上定義了布朗運動,後來也稱數學上的布朗運動為維納過程。這種過程至今仍是隨機過程的重要研究對象。通常認為,隨機過程一般理論的研究於20世紀30年代才開始。1931年,原蘇聯數學家柯爾莫戈羅夫發表了《機率論的解析方法》;1934年,辛欽發表了《平穩過程的相關理論》。這兩篇重要論文為馬爾可夫過程和平穩過程奠定了理論基礎。稍後,法國數學家萊維從樣本函式角度研究隨機過程,引進一般可加過程並研究了它的樣本函式結構,他出版的關於布朗運動與可加過程的兩本書中蘊含著豐富的機率思想。1953年,美國數學家J.L.杜布出版的著作《隨機過程論》中系統且嚴格地敘述了隨機過程的基本理論。他的工作推動了鞅理論的發展。1953年日本數學家伊藤清建立了關於布朗運動的隨機微分方程的理論,定義了對布朗運動的一種隨機積分——伊藤積分,為研究馬爾可夫過程開闢了新的道路。近年來由於鞅論的進展,人們討論了關於半鞅的隨機微分方程,而流形上的隨機微分方程理論正方興未艾。20世紀60年代,法國學派基於馬爾可夫過程和位勢理論中的一些思想與結果,在相當大的程度上發展了隨機過程的一般理論,包括截定理與過程的投影理論等,中國學者在平穩過程、馬爾可夫過程、鞅論、極限定理、隨機微分方程等方面都做出了較好的工作。
