基本介紹
- 中文名:面積律構型
- 外文名:area ruled configuration
- 提出者:R.T.惠特科姆
- 提出時間:1952年
- 分類:跨聲速面積律和超聲速面積律
- 目的:提升飛行器飛行性能
基本理論,分類,跨音速面積律,超音速面積律,套用,全部修形和部分修形,修形馬赫數的選擇,
基本理論
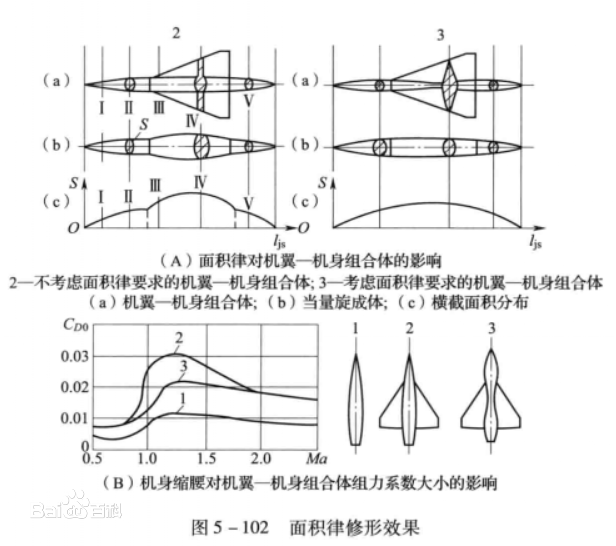
飛機作跨音速飛行時,其零升阻力在音速附近總要顯著上升,直到某一超音速後才隨馬赫數增大而下降一些。阻力上升的遲早和上升量的大小,與飛機的橫截面積沿其縱軸的分布情況有關。實驗發現,細長旋成體的阻力上升得最晚(對應於阻力上升的馬赫數可大於1.0),上升量也最小。帶機翼的旋成體阻力上升較早(對應的馬赫數可小於0.9),上升量也數倍於光滑的旋成體。理論與實驗都已證明,如果把一架飛機的橫截面積折算成一個當量的旋成體,而該當量旋成體的橫截面積沿縱軸變化平緩(無突變),則飛機在跨音速範圍內的阻力上升就可以推遲,上升量也可減小,這就是跨音速面積律。為滿足橫截面積無突變的要求,在設計時可將有機翼之處的機身橫截面縮小,甚至還可把機翼之前的那段機身放大些。
在超音速時也有面積律。這個面積律也要求翼身組合體的當量旋成體的截面積沿縱軸無突變,但應順著馬赫線截取組合體的截面積,而不是橫截面積。過機身縱軸上一點,可以作一個馬赫錐,錐上每一條母線都是馬赫線,因而截面也就有無數個。超音速面積律所說的截面積,就是這樣多截面的平均值。
分類
面積律是為保證飛機在高亞聲速和跨聲速範圍內飛行的阻力最小,飛機所有部件的截面疊在一起的部分(從機頭到機尾)應該相當於一個最小阻力的當量旋成體(稱為西亞斯一哈克旋成體)截面積的分布(或分布曲線比較光滑而無不規則變化),跨超聲速阻力明顯減小。
面積律分為跨聲速面積律和超聲速面積律。
跨音速面積律
1952年R.T.惠特科姆通過風洞實驗發現,當飛行馬赫數接近於1時,飛行器的零升波阻力是飛行器橫截面積(與飛行方向垂直的截面積)分布的函式,而且近似地等於具有相同橫截面積分布的旋成體(稱為當量旋成體)的零升波阻力。因此,可根據最小波阻力旋成體的橫截面積分布來調整飛行器的橫截面積,以獲得較小的波阻力。機翼-機身組合體橫截面積 A-A與其當量旋成體的對應橫截面積 B-B相等。
因為光滑(母線無反曲)旋成體的波阻最小,所以為了降低飛行器跨音速飛行時的零升波阻力,可以修改機身橫截面積沿縱軸的分布,例如縮小機翼、尾翼與機身連線區的機身橫截面積和增大機翼、尾翼前後方的機身橫截面積,形成蜂腰形機身,使飛行器當量旋成體的橫截面積分布與最小波阻旋成體的相接近或做到儘量光滑。
美國的YF-102戰鬥機在1954年試飛時由於跨音速波阻力過大而未超過音速,後來採用了跨音速面積律和其他措施,使其改型機YF-102A於同年試飛時順利地超過音速。這是世界上第一架採用跨音速面積律的飛機。
超音速面積律
1953年美國空氣動力學家O.瓊斯提出超音速面積律。與跨音速面積律相比,所不同的是決定超音速飛行時飛行器的零升波阻力的截面積不是飛行器的橫截面積,而是在給定的飛行馬赫數下通過機身縱軸上某一點的後馬赫錐的切平面(稱馬赫平面)所切割的飛行器截面積。
由於每個子午角θ都對應著一個馬赫平面,不同子午角θ的馬赫平面所切割的飛行器截面積是不同的,因此應取θ從零到2π中各馬赫平面所切割飛行器截面積投影的平均值作為機身縱軸上這一點的當量旋成體的截面積。同樣,為了降低超音速飛行時飛行器的零升波阻力,必須使這一當量截面積沿縱軸的分布儘量光滑。
套用
面積律給跨、超聲速飛機減阻提出了一個簡單的概念和有效的途徑。在許多飛機上得到實際套用,證明其確切的減阻效果。在飛機方案設計階段進行各種面積律修形可以取得很好的效果。
全部修形和部分修形
按面積律的要求修形往往會將機身的體積削去太多而影響機身受力構件布置和內部空間利用,實現起來較困難,因此採用部分修形。但部分修形效果比全部修形的要差。部分(50%)修形、全部修形和基本機身阻力係數比較,50%修形機身獲得超過50%的效果。
修形馬赫數的選擇
套用超聲速面積律時如何選擇馬赫數?對於具體的飛機,由於斜切的面積分布不同,修形馬赫數的選擇需要具體分析。圖1表示某機翼機身組合體的自由飛行試驗結果,模型1為基本模型,模型2~模型4分別為按Ma=1.0,1.2,1.41修形。由圖1可知採用跨聲速面積律修形可能出現在某些馬赫數時阻力偏高,而採用Ma=1.41修形可得到較低的CDO值。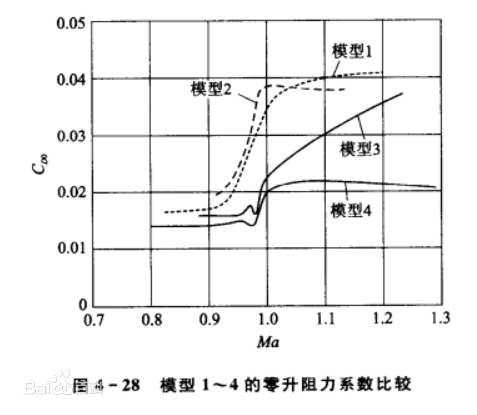

圖1 某機翼機身組合體的自由飛行試驗結果