面積割補法作圖(construction by excision and fill vacancy area)是作圖解題的一種常用方法。關於面積的作圖，多數是等積變形的問題，就是要改變直線形的形狀，但不許改變它的面積。這種問題除一部分須用代數解析外，通常可套用定理“兩三角形同底而頂點都在底的一條平行線上，那么一定等積”，就是“同底等高的兩三角形等積”，在原形上割下一三角形，再利用平行線補以同底等高的另一三角形，使面積不變，而成所需的另一形狀。打一個比方，好象沿江的沙灘，受到暴風雨的侵襲，往往西沙塌掉一塊，東沙漲起一塊，地形雖變，但面積不變。這樣的作圖方法叫做面積割補法。
基本介紹
- 中文名：面積割補法作圖
- 外文名：construction by excision and fill vacancy area
- 所屬學科：數學
- 所屬問題：平面幾何(尺規作圖)
- 簡介：作圖解題的一種常用方法
基本介紹,例題解析,
基本介紹
面積割補法作圖是作圖解題的一種常用方法。對於等積變形的作圖題，通常在給定圖形或某一確定圖形上割下一個三角形，再藉助平行線補上一個同底等高的另一個三角形，使面積不變，從而完成所求作圖形。
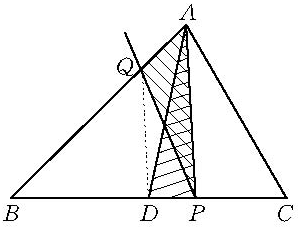圖1例如，過△ABC的底邊BC上一定點P求作一條直線，使它分△ABC的面積為相等的兩部分。其思路要點是：因為中線AD平分△ABC的面積，所以首先作中線AD，假設PQ平分△ABC的面積(如圖1)，在△ADC中，割去△APD，再補上△APQ，由於△APD與△APQ同底等高，面積相等，所以符合條件的PQ可以作出，本題一解。
例題解析
【例1】如圖，在四邊形ABCD中，DE是與BC相交的直線，在BC的延長線上求作一點F，使△DEF的面積等於四邊形ABCD的面積。
作法(1)連結BD，過點A作AG//BD，交CB的延長線於G，連結DG；
(2)延長BC到F，使CF=EG，連結DF，
則△DEF就是所求作的三角形。
證明和討論略。
圖2說明 本題是套用“面積割補法”作圖的，根據同底等高的兩個三角形面積相等的性質，把△BAD等積變形為△BGD，再根據等底同高的兩個三角形面積相等的性質，把△DGE等積變形為△DCF，在解題過程中用了兩種不同的等積變形的方法。
【例2】求作一矩形使和已知三角形等積，且使矩形的一邊等於定長l。
分析 先把△ABC等積變形為底等於l的△GBD，然後再以△GBD的底為長，高的一半為寬，作矩形即可。．
作法 在BC(或其延長線)上取BD=l，連AD，過點C作AD平行線交BA(或其延長線)於點G；過點G作GH⊥BD，垂足為H；再以BD為長、
為寬作矩形BDEF，則矩形BDEF即為所求。
圖3證略。
【例3】把一個已知四邊形ABCD改成一個等積的矩形，使矩形的底等於定長l。
分析 先把四邊形ABCD改成一個等積三角形，然後解之。
圖4作法 連BD，過點C作BD平行線交AB延長線於點H，在AH(或其延長線)上取AE=l，過點H作HK∥DE，交AD延長線於點K，過點KL⊥AE，垂足為L。再以AE為長、 
為寬作矩形AEFG，則矩形AEFG即為所求。
證略。
