非累贅取樣編碼是一種編碼方法,它包括多項式預測器編碼,多項式內插法和心電圖適應性取樣法等。
基本介紹
- 中文名:非累贅取樣編碼
- 外文名:Non-cumulative sampling code
非累贅取樣編碼法,多項式預測器,多項式內插法,
非累贅取樣編碼法
以下將探討兩類非累贅取樣編碼法:多項式預測器及多項式內插法
多項式預測器所採取的方法是:測試下一個取樣看看他是不是落在一個n次多項市所展開的範圍內。最常被使用的是0次及1次多項式。著名的串長編碼(run-length coding)則是0次多項式的一個特別版本。
多項式內插法與多項式預測器類似,唯一的不同是他允許的機動的改變其所展開的範圍。一次多項式內插法,又名善行算法,是用許多線段來取代原波形。
多項式預測器
非累贅取樣壓縮法中多項是預測器算是相當早期的發明。早在60年代早期便有許多論文在討論他並且實際套用在許多實驗上,其中在常被使用到的是0階預測器及1階預測器。
在多項式預測器里,下一個取樣被預測是在一個n次多項式的範圍內。數學上我們可以表示如下,其中表示所預測的下一個取樣值,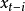 為
為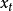 之前的第
之前的第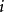 個取樣
個取樣
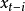
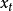
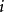
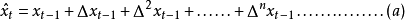
其中

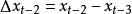
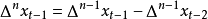
以下我們將更詳細的介紹多項是預測器中最常見的兩種:0次預測器及1次預測器。
0次預測器
0次預測器的式子為:
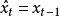
換句話說,我們預測下一個取樣值是和前一個取樣值一樣。在實際的設計上,我們得在這個預測值的上下個加上一個誤差容忍範圍,亦即這個預測值並不是單一個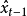 值,而是介於
值,而是介於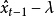 到
到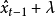 的一個範圍,其中
的一個範圍,其中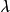 的值由設計人自行根據能容許的誤差程度及所需要的壓縮比來設定。只要
的值由設計人自行根據能容許的誤差程度及所需要的壓縮比來設定。只要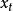 是落在
是落在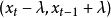 這個範圍之內,
這個範圍之內,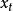 便會被當成是累贅取樣。
便會被當成是累贅取樣。
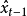
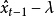
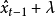
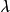
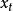
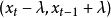
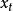
以下為0次預測器之算法:
算法:0次預測器
算法:0次預測器
第一步:儲存便傳送第一個取樣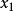 :
: ;
;
第二步:讀入下一個取樣,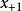 ;第三步:如果
;第三步:如果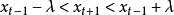 則
則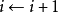 ;回到第二步;否則儲存並傳送
;回到第二步;否則儲存並傳送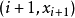 ;
;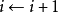 ;回到第二步;
;回到第二步;
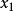

第二步:讀入下一個取樣,
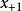
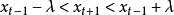
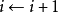
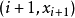
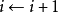
1次預測器
一次預測器的式子為:
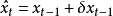
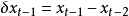
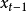
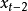
實際上的算法也必須加上一個誤差容忍範圍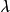 。
。
算法:1次預測器
算法:1次預測器
第一步:儲存便傳送第一個取樣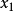 :
: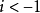 ;
;
第二步:儲存並傳送第二個取樣,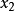 ;
;
第三步:如果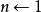 ;
;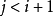 ;讀入下一取樣
;讀入下一取樣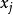 ;
;
第三步:若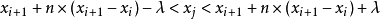 ,則
,則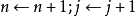 讀入下一個取樣
讀入下一個取樣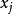 並回到第四步;
並回到第四步;
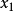
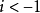
第二步:儲存並傳送第二個取樣,
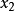
第三步:如果
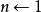
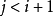
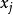
第三步:若
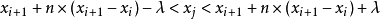
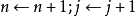
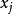
否則
儲存並傳送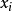 及其發生時間;
及其發生時間;
儲存並傳送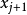 ;
;
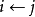 回到第三步;
回到第三步;
儲存並傳送
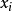
儲存並傳送
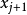
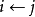
多項式內插法
我們也討論0次與1次的內插法。0次內插法與0次預測器除了前者的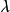 可以改變外,其餘完全一樣。機動性調整
可以改變外,其餘完全一樣。機動性調整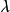 值可以讓累贅取樣更多。
值可以讓累贅取樣更多。
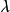
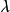
一次內插法又稱為扇形算法(fan algorithm),從60年代被提出以來即受到很大的注意,也有很多成功的套用。基本上他和一次預測器類似。不同的是他的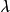 值根據取樣的情況而改變。
值根據取樣的情況而改變。
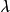
算法:扇形算法
第一步: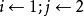
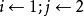
設定第一個取樣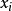 為非累贅取樣:
為非累贅取樣:
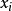
第二步:以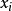 為心向
為心向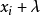 及
及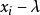 展開一扇形;
展開一扇形;
第三步:如果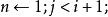 讀入下一取樣
讀入下一取樣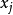 ;第三步:若
;第三步:若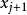 落在扇形內,則
落在扇形內,則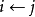 ;
;
回到第二步;
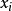
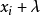
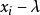
第三步:如果
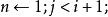
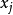
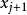
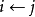
回到第二步;
否則;設定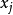 為非累贅取樣;
為非累贅取樣;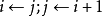 ;回到第二步;
;回到第二步;
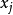
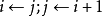
第四步:重複以上的步驟直到編碼完所有取樣點;
第五步:送出每個非累贅取樣及其發生時間;
第六步:接收端收到非累贅取樣後以線段將相鄰之非累贅取樣連起來即可。
