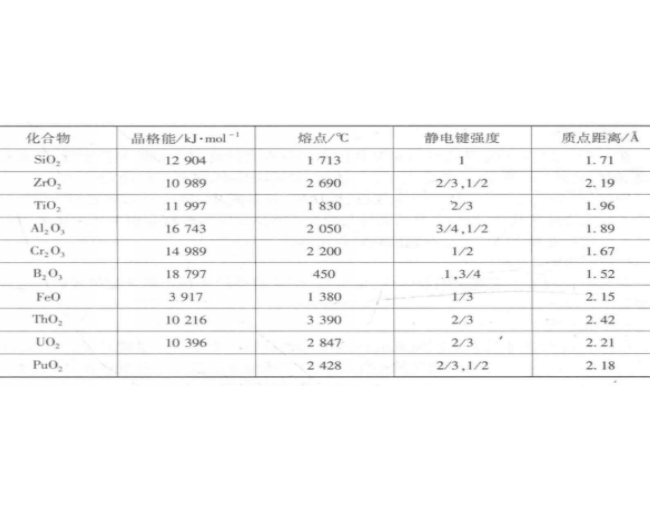
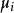靜電鍵強度

靜電鍵強度

正、負離子間的鍵強除了可以用晶格能來衡量外，還可以用靜電鍵強度來粗略估計，從正離子分配給每一個配位負離子的電荷S稱為靜電鍵強度

基本介紹

  • 中文名：靜電鍵強度
  • 計算方法：離子的電荷數除以配位數
  • 衡量對象：正、負離子間的鍵強
  • 相關概念：配位數，電荷數鮑林規則等
基本介紹,鮑林規則,第一規則,第二規則(電價規則),第三規則,第四規則,第五規則,

基本介紹

正、負離子間的鍵強除了可以用晶格能來衡量外，還可以用靜電鍵強度來粗略估計，從正離子分配給每一個配位負離子的電荷S稱為靜電鍵強度，表示為
式中，
為正離子的電荷數，
為其配位數。
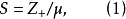
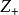
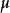
例如，對於NaCl離子晶體來說，靜電鍵強度為1/6，其晶格能為788.1 kJ/mol，均是比較低的，可見兩者基本對應。
MgO晶體也是以離子鍵為主的化合物，其靜電鍵強度為1/3(2/6)，比NaCl離子晶體的靜電鍵強度大，因此MgO晶體的結構穩定性和力學強度均比NaCl晶體高，如其熔點高達2 800 ℃，而NaCl晶體的熔點僅為801℃。
TiO2：靜電鍵強度為2/3(4/6)，熔點1 830℃。
UO2：靜電鍵強度為1/2(4/8)，熔點2 847℃。
Al2O3：靜電鍵強度為1/2(3/6)，熔點2 050 ℃。
一些化合物的靜電鍵強度和熔點見表1。
表1 一些氧化物和矽酸鹽的晶格能與熔點等特性的關係表
化合物
晶格能/kJ·mol-1
熔點/℃
靜電鍵強度
質點距離/A
BeO
4 443~4456
2 570
2/3，1/2
1.66
MgO
3 791~3 930
2 800
1/3
2.10
CaO
3 401~3 520
2 587
1/9，1/4
2.38
SrO
3 223
2 457
1/3
2.59
BaO
3 054
1 923
1/3
2.75
SiO2
12 904
1713
1
1.71
ZrO2
10 989
2 690
2/3，1/2
2.19
TiO2
11 997
1 830
2/3
1.96
Al2O3
16 743
2 050
3/4，1/2
1.89
Cr2O3
14 989
2 200
1/2
1.67
B2O3
18 797
450
1，3/4
1.52
FeO
3 917
1 380
1/3
2.15
ThO2
10 216
3 390
2/3
2.42
UO2
10 396
2 847
2/3
2.21
PuO2
2 428
2/3，1/2
2.18

鮑林規則

為了分析比較複雜的離子晶體結構，鮑林於1928年從大量數據以及晶格能公式所反映的原理中歸納出五個規則。

第一規則

在正離子周圍形成一個負離子多面體，正、負離子間的距離取決於離子半徑之和，而配位數取決於正、負離子半徑之比。
當正、負離子半徑之比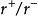
為1~0.732(接近1)時，正離子配位數為8，負離子位於立方體的8個頂點上而構成骨架。當
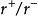為0.732~0.414(接近0.5)時，正離子配位數為6，負離子位於八面體的頂點。當
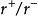為0.414~0.225(接近0.25)時，正離子配位數為4，負離子位於四面體的頂點。當再降低
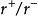時，正離子配位數減為3或2，負離子位於三角形的頂點或啞鈴形頂點。

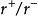
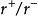
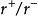
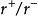
第二規則(電價規則)

在一個穩定的離子化合物結構中，每一個負離子的電價等於或接近於與之鄰近的正離子靜電鍵強度之和，即
式中：
——負離子電荷數(電價)；
——第
種正離子的靜電鍵強度；
——第
種正離子的電價；
——第
種正離子的配位數。
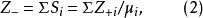
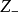
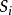
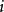
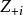
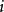
利用電價規則，可以檢驗離子晶體結構的穩定性。即計算每個負離子所得到的靜電鍵強度的總和，並且看它是否與其電價相等；如果相等，則結構穩定。例如，在金紅石TiO2中(正、負離子配位數分別是6和3)，從某一個O2-至Ti4+的靜電鍵強度為S=4/6=2/3，而每一個O2-同時為3個配位八面體的頂點，因此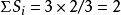
，正好等於O2-的電價。這證明金紅石結構是穩定的。

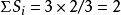
第三規則

在一個配位結構中，共用棱特別是共用面的存在會降低這個結構的穩定性，尤其是電價高、配位數低的正離子，該效應更顯著。因此，共用棱越少，結構就越穩定。
例如，在TiO2的三種變體——金紅石、板鈦礦、銳鈦礦中，每一個氧離子O2-都為三個[TiO6]8-八面體所共用，但每一個八面體與相鄰八面體共用的棱數分別為2、3和4。因此，金紅石型結構是很多AB2型化合物的穩定存在形式。

第四規則

在含有一種以上正離子的晶體中，電價高、配位數低的那些正離子配位多面體之間應當儘量不連線。

第五規則

在同一晶體中，本質上不同組成的構造單元數目趨向於最少。這就是說，參加晶體結構的正負離子應儘可能少，否則多種多樣的多面體就很難形成一個有規律排列的、統一的晶體結構骨架。這也意味著結構中一切化學上相同的負離子應具有相似的周圍環境。因此，儘管電價規則允許負離子周圍有幾種安排正離子的方式，但是其中可以實現的只有一種。例如，在剛玉α-Al2O3結構中，正、負離子配位數分別是6和4，所有O2-的周圍都有4個Al3+，所有的Al3+周圍都有6個O2-，所有的Al3+－O2-間靜電鍵強度均為1//2價。
鮑林規則對絕大多數離子晶體都適用，但是不適用於以共價鍵為主的晶體。

相關詞條

熱門詞條

聯絡我們