基本介紹
定義,從量子光學理論探討氣體原子的電極化率,電磁場與原子的相互作用,氣體介質原子在振盪電磁場中的極化,結論,
定義
有些電介質的P和E呈現出複雜的非線性關係,類似於磁滯回線,稱為電滯回線,這種性質稱為鐵電性,如酒石酸鉀鈉,鈦酸鋇等鐵電體。鐵電性一般只存在於一定溫度範圍內,當溫度超過臨界的居里溫度時,鐵電性隨之消失。有些晶體材料如水晶等的極化各向異性,P和E的關係很複雜,其電極化率是一個二階張量。用符號χe表示,χe與相對電容率εr的關係為εr=1+χe。
從量子光學理論探討氣體原子的電極化率
電磁場與原子的相互作用
原子序數為 Z的中性原子的電偶極矩
考慮一個原子序數為 Z 的中性原子 ,以原子核為坐標原點 ,各電子在某一時刻的位置為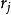 ,見圖 1。
,見圖 1。
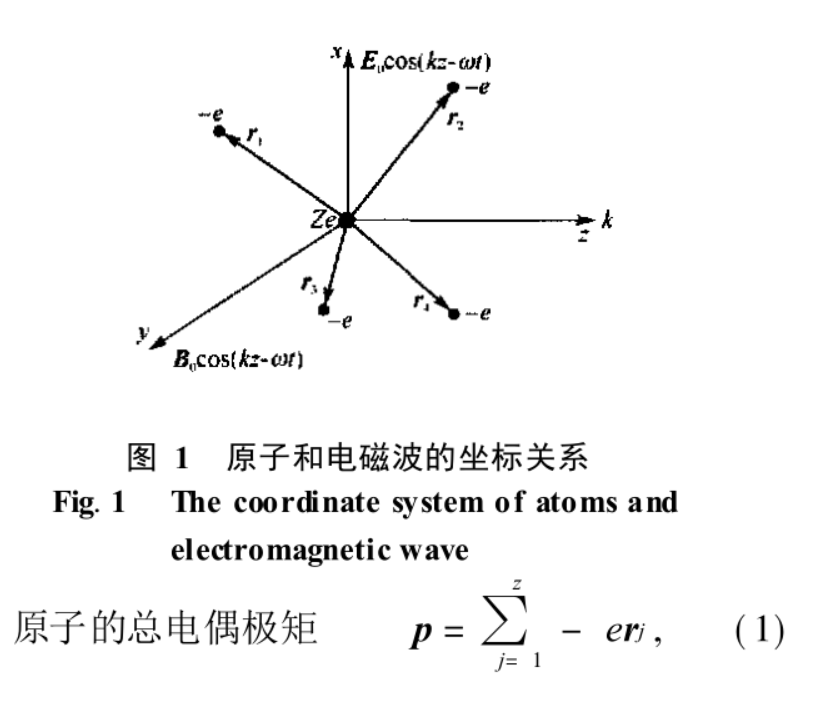 圖1
圖1原子的總電偶極矩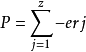 ,(1)
,(1)
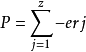
令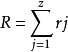 ,則
,則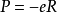 (2)
(2)
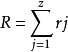
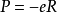
對相互作用哈密頓量的主要貢獻來自電偶極矩在電場E0coskt中的勢能,寫成
Η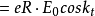 (3)
(3)
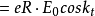
在這裡作如下簡化:
原子中電子運動的玻爾半徑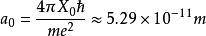 ,式中m是電子質量。倘若電磁波頻率g=10Hz,則電磁波波長
,式中m是電子質量。倘若電磁波頻率g=10Hz,則電磁波波長 ,所以在整個原子線度內電磁場空間變化很小,故有
,所以在整個原子線度內電磁場空間變化很小,故有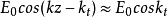
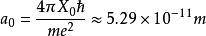

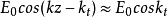
二能級原子相互作用哈密頓算符的矩陣
考慮二能級原子能級1的波函式J1(r,t),本徵能量為E1,本徵態為j1(r);能級2的波函式J2(r,t),本徵能量為E2,本徵態為j2(r),原子波數的普遍形式為

從式(3)知相互作用哈密頓量是實量,且存在奇宇稱性,即當用-rj代替rj,對核進行反演時,Η改變符號。
定義矩陣元

由Η的奇宇稱性知,g11,g22的被積函式是位置的奇函式,故對全部空間積分必為零,結合g12和g21的定義,得
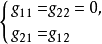
由於圖1中E沿x方向,將(3)式代入(5)式中的g12,得

(7)式中
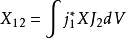
X是R的x分量,即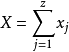 。積分要遍及所有的電子坐標。令
。積分要遍及所有的電子坐標。令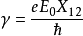 ,則
,則
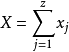
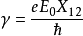

氣體介質原子在振盪電磁場中的極化
單個原子的電偶極矩複數表示
原子的電偶極矩為

將式(4)代入式(10),得
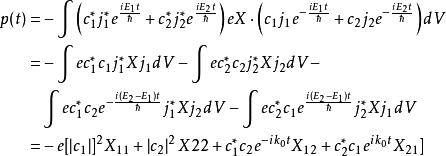
為清晰起見,把函式 ,
, ,
, ,
, 中的自變數t,r省去了。由式(5)和(6)的定義及性質,上述P(t)中X11,X22,X12,X21也有類似性質,即
中的自變數t,r省去了。由式(5)和(6)的定義及性質,上述P(t)中X11,X22,X12,X21也有類似性質,即





所以

現在來示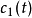 ,
, ,由式(4)得
,由式(4)得
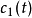


左邊乘以 後對整個空間積分,得
後對整個空間積分,得


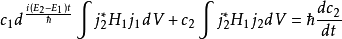
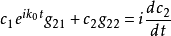
利用式(6)性質得
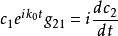
 公式(16)到(20)
公式(16)到(20)氣體原子的電極化率
氣體的巨觀電極化強度為
 公式(21)(22)
公式(21)(22) 公式(23)(24)
公式(23)(24)結論
由於電磁場對原子的相互作用的影響主要是電場對原子的作用 ,磁場對原子的作用遠小於電場對原子的作用 ,所以只考慮了電場對原子的相互作用 ,特別是頻率較高的光波更加適用此近似。通過引入量子光學的統計波理論 ,從氣體介質在電磁場中極化的電極化強度定義出發 ,經過詳細推導 ,最後得出氣體介質在振盪電磁場中極化的電極化率 i的表達式。並且經過與特殊情況比較 ,作者認為這一結果的表達式是正確的。 通過本文的描述使讀者對氣體介質在振盪電磁場中產生的極化有一個較全面的認識和理解 ,對新材料在記憶、貯存和壓電效應等方面的套用研究都有較高的參考價值。