電力系統運行約束

電力系統運行約束(AGC)是時時刻刻保證發電與負荷平衡、維持電力系統頻率質量的重要技術手段。

基本介紹

• 中文名：電力系統運行約束
• 外文名：AGC
• 系統：發電與負荷平衡、維持電力系統
• 性質：技術手段

研究背景

電力系統運行約束(AGC)是時時刻刻保證發電與負荷平衡、維持電力系統頻率質量的重要技術手段。近年來，我國電力系統AGC工作取得了很大的進展，其中一個重要標誌是大量的發電機組具備了投入AGC運行的條件。以華東電網為例，到2002年底，全國具備投入AGC運行的發電機組容量占全網統調裝機總容量的55%，AGC可調容量占全網統調最高負荷的25.99%。AGC可調容量的大幅增加為電力系統安全、優質、經濟運行提供了良好的條件。但是，在日常運行中，電力系統中應保持多少AGC可調容量，這是一個需要認真解決的問題。當然，系統中保有大量的AGC可調容量，對維持電力系統頻率質量有好處，但發電機組保持AGC可調容量會減少正常的發電量，機會成本提高；投入AGC運行，機組的運行費用增加。在電力市場的環境中，AGC是發電機組向電網提供調節服務的技術手段，機組投入AGC運行是要在輔助服務市場中收取費用的。因此，作為電力系統的控制者和電力市場的運營者——電力調度交易中心，必須了解在電力系統運行中對AGC調節容量的需求，關按此需求採購或安排發電機組的AGC可調容量，這樣才能做到既保證電力系統的安全，又降低運行費用。

概述

電力系統頻率變化主要是由負荷波動引起的。根據對負荷分量的分析，可以得到各種負荷的分量和對應的調整方式。第1種負荷分量：變化周期在10s以內、變化幅度較小的負荷分量，稱為隨機波動的負荷分量，對應的調整方式是發電機組的一次調節；第2種負荷分量：變化周期在10s到數分鐘之間的負荷分量，稱為分鐘級負荷分量，對應的調整方式是AGC；第3種負荷分量：變化緩慢的持續變動負荷分量，又可細分為第4種負荷分量(基點負荷分量)和第5種負荷分量(爬坡負荷分量)。由於對第3種負荷分量的調整並不是必須採用AGC控制，可以採用人工控制，因而本文對AGC調節需求的分析僅考慮平衡分鐘級負荷分量的需要。但是，第3種負荷分量的調整在一段時間內(10多分鐘，乃至數十分鐘)對發電機出力的要求是單調增加或單調減小的。大多數發電機組都能適應這樣的要求，若能採用AGC方式對大量調節速率較低的發電機組進行控制，精確實現對第3種負荷分量的調整，則有利於減輕分鐘級負荷分量調整的壓力。確定AGC調節容量的要求，與負荷預測相似，是依據過去事實的規律和對未來的預測。與負荷預測不同的是，負荷預測考察的是負荷的幅值，而AGC調節的目標是平衡負荷分鐘級的波動。因此，確定AGC調節容量的依據是分鐘級負荷波動的幅值和速率。

分離分鐘級負荷分量的算法

2.1 滾動平均法滾動平均法通過對每一個負荷幅值前、後一段數值滾動求平均，由此得到一條平滑的負荷曲線。滾動求平均的算式為：

　　式中：LFT是經滾動平均法平滑處理後時刻t的負荷值；Lt是原時刻t的負荷值；2M是滾動求平均的負荷幅值的個數。
M的取值與負荷幅值的採樣和存儲周期以及滾動求平均的時段長度有關。例如：負荷幅值的採樣和存儲周期為15s，滾動求平均的時段長度為15min，則滾動平均所需的負荷幅值個數為60，由此，取M=30。滾動求平均的時段長度不同，則求得的負荷曲線也不同，圖1顯示了用15min，30min，60min等3個不同時段長度滾動求平均得到的同一時段的負荷曲線。從圖中可以看出，滾動求平均的時段越長，則求得的負荷曲線變化越平緩。求得平滑的負荷曲線後，分鐘級負荷分量的有關參數可以用以下方法求出。
　　2.1.1 分鐘級負荷分量的幅值
由於負荷的隨機波動已由電力系統的一次調頻作用所平衡，Lt與對應時刻的LF1之差，即為分鐘級負荷分量的幅值。分鐘級負荷分量的求得也與滾動求平均的時段長度有著密切的關係，圖2顯示了用15min，30min，60min等3個不同時段長度滾動求平均求得的同一時估的分鐘級負荷分量。從圖中可以看出，滾動求平均的時段越長，則求得的分鐘級負荷分量的幅度越大。
　　2.1.2 分鐘級負荷分量的變化速率
取相鄰分鐘的分鐘級負荷分量平均值Lm與Lm+1之差作為分鐘級負荷分量的變化率。通過用不同的時段長度來滾動求平均，可以得到不同的分鐘級和持續變化的負荷分量(基點負荷分量和爬坡負荷分量)，從中可以看出分鐘級和持續變化的負荷分量之間的界線不是絕對的，而這兩者是一對矛盾，滾動求平均的時段拉長，持續變化的負荷分量的變化趨平緩，但分鐘級負荷分量的變化幅度變大，這樣，將減輕系統對持續變化的負荷分量的調節壓力，但加重對AGC調節的需求；反之，縮短滾動求平均的時段，則將減輕系統對AGC調節的需求，但加重對其餘的負荷分量的調節壓力。因此，段根據負荷的特性，適當選擇滾動求平均的時段長度。根據經驗，對於一般特性的負荷，滾動求平均的時段長度選擇15min較為適宜；但對於有較大衝擊負荷(如大型鋼廠)的控制區，則選擇較生長期的時段長度(如30min)較為適宜。
2.2 時段平均法
時段平均法通過對一段時間(時間段的長度可以是5min，10min,15min)的負荷幅值求平均，得到一組每5min離散的負荷幅值；經線性插值後，得到一條由爬坡負荷組成的負荷曲線(見圖3的曲線2)，並用下述方法求出分鐘級負荷分量的有關參數。
　　2.2.1 分鐘級負荷分量的幅值
與滾動平均法相同，實際負荷Lt(圖3的曲線1)與對應時刻t爬坡負荷(圖3的曲線2)之差，即為分鐘級負荷分量的幅值。圖3表示了以5min為時段長度，用時段平均法分離分鐘級負荷分量的效果。
2.2.2 分鐘級負荷分量的變化速率
與滾動平均法相同，求得分鐘級負荷分量後，以分鐘級負荷分量相鄰的分鐘幅度值平均之差作為分鐘級負荷分量的變化率。
使用時段平均法同樣可以通過用不同的時段長度求平均，得到不同分鐘級和持續變化的負荷分量。時段長度的變化對分離分鐘級和持續變化的負荷分量的影響，與滾動平均法是相似的。如果時段較短，分離所得的分鐘級負荷分量幅度較小，但持續變化的負荷分量變換方向較頻繁，對另一部分發電機組的調節帶來困難。圖4、圖5分別表示用5min時段和15min時段對同一組負荷數據分離所得的持續變化的負荷分量，從圖4中可見，曲線有多處5min就改變了方向。因此，須根據負荷的特性，適當選擇求平均時段長度，一般以選擇15min為宜。
　除了上述2種方法外，還有多種方法可以用於分離分鐘級負荷分量和持續變化的負荷分量，如多項式按按擬合，可以得到精確而平滑的負荷曲線；但由於在1d中負荷的變化規律是不同的，需要選擇不同的回歸模型來進行擬合，處理會變得很複雜。因此，滾動平均法和時段平均法是兩種簡單而實用的方法。

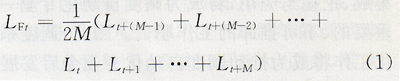電力系統運行約束

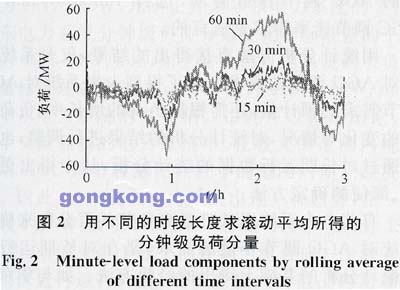電力系統運行約束

電力系統運行約束

電力系統運行約束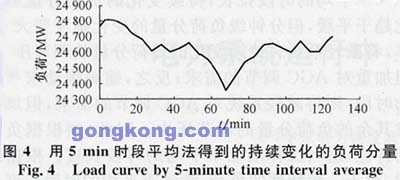

電力系統運行約束

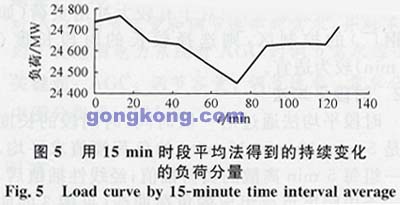電力系統運行約束

對AGC調節需求的統計分析

通過利用上述方法，可以得到與負荷幅值採樣和存儲周期相應的各個時刻的調節負荷分量和每分鐘的調節負荷變化率。由此可以確定系統對AGC調節容量及速率的需求。
通過各種方法分離而得的調節負荷分量及其變化率的最大值代表了系統對調節服務的容量及速率的最高需求。但是，用這種方法來確定系統對調節服務的容量及速率的需求，容易受到特殊的系統運行工況、甚至壞數據的干擾，所得的結果往往不能代表正常情況下的系統需求，有時甚至是錯誤的。圖6、圖7分別表示了對華東電網某日的負荷幅值用滾動平均法求得的分鐘級負荷分量和分鐘級負荷分量變化率的分布情況。從圖中可看出，分鐘級負荷分量的最大值約為384MW，而分鐘級負荷分量變化率的最大值大約為-235MW/min。但這種最大值在1d中僅為個別情況，而絕大部分的情況遠小於最大值。因此，以最大值來確定系統對調節服務及其速率的需求是不經濟的，也是沒有必要的，應該採用統計分析的方法，從中找出分布規律。
　根據統計學的原理，一組服從常態分配的樣本數據，分布在(-2.5σ，2.5σ)範圍之內的樣本點約占95%(σ為該組樣本數據的標準差)，而分布在(-3σ，3σ)範圍之內的樣本點約占99.8%。經過對圖6、圖7所示的兩組數據的統計分析，得到分鐘級負荷分量及其變化率的標準差分別為60MW和46MW/min。從圖6可以看出，華東電網的分鐘級負荷分量絕大多數分布在-180MW至180MW之間；分鐘級負荷分量的變化率則絕大多數分布在-138MW/min到138MW/min之間，完全符合統計規律。因此，選擇±180MW為該日華東電力系統的AGC調節容量需求，選擇138MW/min為AGC調節速率需求是適宜的。
用統計分析方法直接得出的結果，僅是系統過去對AGC調節的需求。為了得到未來系統對AGC調節需求的預計值，還需根據負荷的增長率、負荷特性的變化等情況，對統計分析的結果進行調整，也可以通過對長期運行數據的統計分析，從中得出更直接、簡便的確定方法。
有些電力系統以某日高負荷的百分數來確定系統對AGC調節容量的需求，是在對長期運行數據統計分析的基礎上得出的經驗方法。如與華東電力系統規模相近的美國賓夕法尼亞-新澤西- 馬里蘭(PJM)聯合電力系統，以峰、谷時段最高負荷的1.1%來分別確定峰、谷時段系統對AGC調節的容量需求；而根據對華東電力系統2002年1月份任意抽取的2d負荷數據的統計分析，得到2d中系統對AGC調節的容量需求，分別是系統當日最高負荷的1.04%和1.07%，與PJM方法較為接近。
國外不少電力系統把對AGC調節速率的需求折算成對容量的需求，規定由發電機組提供的AGC調節容量=min(機組實際可調容量、機組的AGC調節速率×m)，m為分鐘數，根據各電力系統的不同情況設定，如紐約ISO設定為5min，加州ISO設定為10min；華東電力系統目前負荷波動速率較高，根據上述統計數據，m=360MW/138(MW.min-1)=2.6min，因此，m應設定為不大於2.6min。

電力系統運行約束

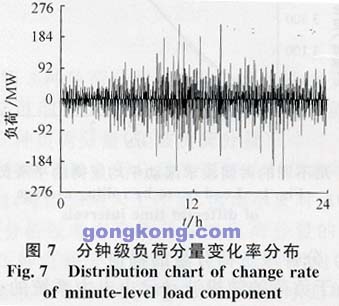電力系統運行約束

不同範圍系統對AGC調節需求的比較

眾所周知，對有功功率的調整是為了平衡發電功率與負荷的偏差，維持電力系統的頻率質量。在電力系統不存在網路約束的條件下，在一個互聯電力系統(交流互聯)的不同地點調整相同容量的有功功率，其效果基本是相同的。因此，對AGC的需求是可以建立在互聯電力系統共享的基礎上。在一個互聯電力系統中統一確定、或分塊確定系統在AGC調節的容量及速率的需求，所需的總量不同。根據美國西部區域輸電組織(Westrto)的研究結論，該區域作為單一控制區對調節服務容量的需求，僅為該區域原各個控制區(共有10個控制區)對AGC調節容量需求總和的約2/5(199/492)。通過對華東電力系統及華東電力系統內各省、市電力系統對AGC調節容量及速率需求的分析研究，可以得出相同的結論。表1給出了對華東及各省、市電力系統分鐘級負荷分量及其變化率的統計分析。
　　根據表中給出的數據可以看出，兩種算法所得的結果比較接近，華東電力系統兩種方法統計所得的分鐘級負荷分量標準差的平均值為66MW，而三省一市電力系統分鐘級負荷分量標準差總和的平均值為131.5MW，幾乎正好是華東電力系統的2倍；華東電力系統分鐘級負荷分量變化率標準差的平均為45.5MW/min，而三省一市電力系統調節負荷分量標準差總和的2d平均值為109.5MW/min，是華東電力系統的2.4倍。由此可以得出結論，在一個交流互聯的電力系統中，在較大的範圍內統一使用AGC調節容量比在較小的範圍內使用經濟得多。因此，近來北美電力系統出現一種趨勢，在一些區域(如West RTO，Desertstar RTO，Ercot ISO等)中，由原來若干較小的控制區組合成一個較大的控制區進行運行控制，可以在較大的範圍內對輔助服務資源實行共享，實現資源的最佳化配置，降低運行費用，提高經濟效益。

電力系統運行約束

結語

電力系統運行中AGC調節器的需求分析總是分為對AGC調節容量和對AGC調節速率的需求分析，這是AGC運行中的重要問題；更是輔助服務市場運作中的重要環節。本文介紹的兩種算法可用於定量分析對AGC調節的需求。但是，該方法所得的電力系統對AGC調節的需求僅滿足平衡分鐘級負荷的波動，對於由於其他原因引起的發電功率與負荷的偏差（如負荷預計偏差、發達機組故障等），應使用其他資源（如備用容量）來平衡。
經過對電力系統運行數據的長期統計分析，可以找出AGC調節容量需求與負荷的關係，並可以將對AGC調節速率的需求轉換為對調節容量的需求，簡化需求分析的工作。
在交流互聯的電力系統中，對AGC調節資源統一使用是降低運行費用的好方法，應予提倡，但必須顧及電網的約束和控制技術條件的限制等因素。