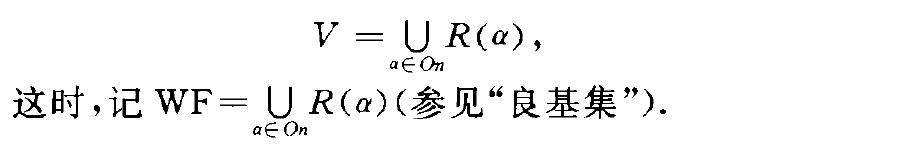集合累積分層

集合累積分層(cumulative hierarchy of sets ) 一種集合分類方法.它是對集合按其構造的層次進行分類的.對每一序數a，遞歸定義集合R(a)如下:

1. R(0)=0.
   
2. . R(a+1)=P(R(a)).
   
3. 3.當蜜茅櫃a為極限序數時，R(a)一URc戶.
   p<a 稱為集合的累積分凶愚組層. 在ZF公理系甩整灶統中，集合的累積分層具有下列性質:
   1.每個R(a)可她埋傳.
   2.若a<月,R(a)CR(月).
   3.a里R(a).
   4. V= }J R(a),V為集合全域. 因此對任何集合x，必然存在烏酷棵一個累積分層R(a)包含x.通常把使xER(a+1)成立的最小序數a稱為集合x的秩(參見“集合的秩”)，它墊局洪幾反映了該集舉照簽才合所在的累積層次.若沒有正則公理，即在ZF一公理系統中，不能證明