隱含狄利克雷分布

隱含狄利克雷分布（Latent Dirichlet Allocation，LDA），是一種主題模型（topic model），它可以將文檔集中每篇文檔的主題按照機率分布的形式給出。

基本介紹

• 中文名：隱含狄利克雷分布
• 外文名：Latent Dirichlet Allocation, LDA
• 類型：機器學習算法，聚類算法
• 提出者：David M. Blei，Andrew Ng，
•  ：M. I. Jordan
• 提出時間：2003年
• 學科：統計學，人工智慧
• 套用：自然語言處理

歷史

LDA首先由Blei, David M.、吳恩達和Jordan, Michael I於2003年提出。

理論與算法

模型

LDA是一種典型的詞袋模型，即它認為一篇文檔是由一組詞構成的一個集合，詞與詞之間沒有順序以及先後的關係。一篇文檔可以包含多個主題，文檔中每一個詞都由其中的一個主題生成。

另外，正如Beta分布是二項式分布的共軛先驗機率分布，狄利克雷分布作為多項式分布的共軛先驗機率分布。因此正如LDA貝葉斯網路結構中所描述的，在LDA模型中一篇文檔生成的方式如下:

從狄利克雷分布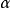中取樣生成文檔i的主題分布

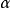
從主題的多項式分布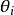中取樣生成文檔i第j個詞的主題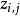

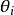
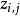
從狄利克雷分布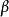中取樣生成主題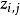的詞語分布

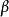
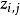
從詞語的多項式分布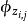中採樣最終生成詞語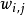

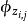
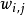
因此整個模型中所有可見變數以及隱藏變數的聯合分布是

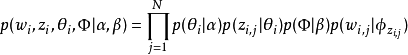
最終一篇文檔的單詞分布的最大似然估計可以通過將上式的{\displaystyle \theta _{i}}以及{\displaystyle \Phi }進行積分和對{\displaystyle z_{i}}進行求和得到

根據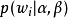的最大似然估計，最終可以通過吉布斯採樣等方法估計出模型中的參數。

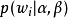
求解

變分貝葉斯估計（variational Bayesian inference）

LDA在提出之初，被設計為使用變分貝葉斯估計，即變分貝葉斯EM進行求解。

馬爾可夫鏈蒙特卡羅（Markov chain Monte Carlo, MCMC）

LDA可以使用MCMC中常見的使用吉布斯採樣（Gibbs Sampling）算法進行求解，其過程如下：

• 首先對所有文檔中的所有詞遍歷一遍，為其都隨機分配一個主題，即z_m,n=k~Mult(1/K),其中m表示第m篇文檔，n表示文檔中的第n個詞，k表示主題，K表示主題的總數，之後將對應的n_m+1, n_m+1, n_k+1, n_k+1, 他們分別表示在m文檔中k主題出現的次數，m文檔中主題數量的和，k主題對應的t詞的次數，k主題對應的總詞數。
  
• 之後對下述操作進行重複疊代。
  
• 對所有文檔中的所有詞進行遍歷，假如當前文檔m的詞t對應主題為k，則n_m-1, n_m-1, n_k-1, n_k-1, 即先拿出當前詞，之後根據LDA中topic sample的機率分布sample出新的主題，在對應的n_m, n_m, n_k, n_k上分別+1。
  
• 疊代完成後輸出主題-詞參數矩陣φ和文檔-主題矩陣θ
  

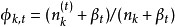
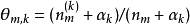
性質

LDA是常見的主題模型之一，是一類無監督學習算法，在訓練時不需要手工標註的訓練集，需要的僅僅是文檔集以及指定主題的數量k即可。此外LDA的另一個優點則是，對於每一個主題均可找出一些詞語來描述它。

套用

LDA在自然語言處理領域，包括文本挖掘（text mining）及其下屬的文本主題識別、文本分類以及文本相似度計算方面有套用。