吉布斯採樣

吉布斯採樣（Gibbs sampling）是統計學中用於馬爾科夫蒙特卡洛（MCMC）的一種算法，用於在難以直接採樣時從某一多變數機率分布中近似抽取樣本序列。該序列可用於近似聯合分布、部分變數的邊緣分布或計算積分（如某一變數的期望值）。某些變數可能為已知變數，故對這些變數並不需要採樣。

基本介紹

• 中文名：吉布斯採樣
• 外文名：Gibbs sampling
• 領域：人工智慧
• 提出者：斯圖爾特·傑曼與唐納德·傑曼
• 目的：聯合分布的採樣
• 有關術語：Metropolis–Hastings算法

簡介

採樣是以一定的機率分布，看發生什麼事件。吉布斯採樣常用於統計推斷（尤其是貝葉斯推斷）之中。這是一種隨機化算法，與最大期望算法等統計推斷中的確定性算法相區別。與其他MCMC算法一樣，吉布斯採樣從馬爾科夫鏈中抽取樣本，可以看作是Metropolis–Hastings算法的特例，可以由馬爾科夫鏈和機率轉移矩陣的性質推出其採樣分布最終收斂於聯合分布。該算法的名稱源於約西亞·威拉德·吉布斯，由斯圖爾特·傑曼與唐納德·傑曼兄弟於1984年提出。吉布斯採樣適用於條件分布比邊緣分布更容易採樣的多變數分布。在統計學和統計物理學中，gibbs抽樣是馬爾可夫鏈蒙特卡爾理論（MCMC）中用來獲取一系列近似等於指定多維機率分布（比如2個或者多個隨機變數的聯合機率分布）觀察樣本的算法。吉布斯採樣算法識別模體的基本原理通過隨機採樣不斷更新模體模型及其在各條輸入序列中出現的位置，最佳化目標函式，當滿足一定的疊代終止條件或者達到最大疊代次數時就得到了最終所求的模體。吉布斯採樣算法是一種啟發式學習方法，它假定每一條序列只包含一個特定長度的模體實例，在各條序列上隨機選取一個模體的起始位置，這樣便得到了初始訓練集，然後通過更新步驟和採樣步驟疊代改進模體模型。假設我們需要從聯合分布中抽取的個樣本，記第i個樣本為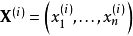。吉布斯採樣的過程則為：

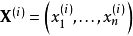
確定初始值；假設已得到樣本，記下一個樣本為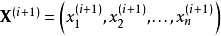，於是可將其看作一個向量，對其中某一分量，可通過在其他分量已知的條件下該分量的機率分布來抽取該分量。對於此條件機率，我們使用樣本，中已得到的分量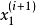到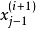以及上一樣本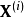中的分量到，即。重複上述過程 k次。如果僅考慮其中部分變數，則可以得到這些變數的邊緣分布。此外，我們還可以對所有樣本求某一變數的平均值來估計該變數的期望。

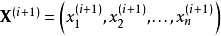
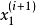
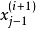
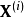
馬爾科夫蒙特卡洛

馬爾科夫蒙特卡洛（Markov chain Monte Carlo，MCMC）方法（含隨機遊走蒙特卡洛方法）是一組用馬氏鏈從隨機分布取樣的算法，之前步驟的作為底本。步數越多，結果越好。創建一個具有期望屬性的馬氏鏈並非難事，難的是如何決定通過多少步可以達到在許可誤差內的穩定分布。一個好的馬氏鏈具有快速混合——從開始階段迅速獲得的一個穩定狀態。因於初始樣本，最常見的MCMC取樣只能近似得到分布。複雜的MCMC改進算法如過往耦合，但是會消耗更多的計算資源和時間。典型用法是模擬一個隨機行走的行人來進行路徑最佳化等。每一步都算作是一個狀態。而統計經過次數最多的地方將在下一步中更有可能為目的地。馬氏蒙特卡洛方法是一種結合了蒙特卡羅法的解決方案。但不同於以往的蒙特卡洛integration是統計獨立的，MCMC中的是統計相關的。MCMC方法是使用馬爾科夫鏈的蒙特卡羅積分，其基本思想是：構造一條Markov鏈使其平穩分布為待估參數的後驗分布，通過這條馬爾科夫鏈產生後驗分布的樣本，並基於馬爾科夫鏈達到平穩分布時的樣本（有效樣本）進行蒙特卡羅積分。

馬爾可夫鏈

馬爾可夫鏈，因安德烈·馬爾可夫（A.A.Markov，1856－1922）得名，是指數學中具有馬爾可夫性質的離散事件隨機過程。該過程中，在給定當前知識或信息的情況下，過去（即當前以前的歷史狀態）對於預測將來（即當前以後的未來狀態）是無關的。在馬爾可夫鏈的每一步，系統根據機率分布，可以從一個狀態變到另一個狀態，也可以保持當前狀態。狀態的改變叫做轉移，與不同的狀態改變相關的機率叫做轉移機率。隨機漫步就是馬爾可夫鏈的例子。隨機漫步中每一步的狀態是在圖形中的點，每一步可以移動到任何一個相鄰的點，在這裡移動到每一個點的機率都是相同的（無論之前漫步路徑是如何的）。