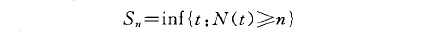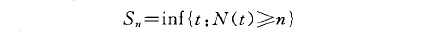隨機點過程是描述按一定統計規律在空間X中隨機地分布的一些點的數學模型。
隨機點過程(stochastic point process or ran-dom point process)簡稱點過程一類數學模型.它是描述按一定統計規律在空間X中隨機地分布的一些點的數學模型.粗略地說,隨機點過程就是隨機的點分布.現實生活中存在著許多這樣的隨機現象,其中人們所關心的隨機事件具有高度局部化的特點,亦即事件的發生可以認為只限於在時間或空間(統稱為狀態空間並記為壓侖產)中的一個很小的範圍內,因此在數學上可以用一個理想化的點來表示.
最常見的情形是狀態空間止見戶取為實數直線卯一(一二,+二)或它的非負部分劣+=[0,+二).因為實數有大小先後的次序,故這樣的點過程又稱為(隨機)事件序列或事件流.
在數學上也可以把隨機點過程定義為一類特殊的隨機測度—隨機計數測度(簡稱計數測度).如同在“隨機測度”條中所述,設觀廠是滿足第二可數公理的局部緊德國數學家豪斯多夫(Hausdorf f , F.)空間.定義在.免廣上的波萊爾代數/}( J)上的計數測度是在緊集上為有限的非負整值測度,人們用一了“奢一)表示它們的全體,男C了)表示}1} ( }})上(關於淡拓撲)的波萊爾代數。於是,努’上的一個隨機點過程就是從基本機率空間(,(Z , ,} , P)到(、不(‘恥/),,(、不))中的一個可測映象守.注意對任意固定的。E,f2,s"(m) E.-}'(})是一計數測度.由於一h'(.}) C}i}l (.}),故隨機點過程是特殊的隨機測度.又若寧是一隨機點過程,則對任意AE.}(}''),P}-'(A)=P{wE},}<})EA}誘導出可測空間(,一才,(壓君廠),男(廠))上的一個機率測度P}-',並稱其為寧的分布.由於寧和它的分布是一一對應的,故又可把一個隨機點過程定義為可測空間(.w'(.0/ ),}(}}'))上的一個機率測度.注意上面定義的點過程是局部有限的,即過程在O~的任意緊集(當莊奢產一貫或男的一個子集時,緊集可用有界集代替)中的點數一定是有限的.
對於狀態空間是劣+=CO,+二)的隨機點過程(不失一般性,可設在時刻t=。沒有點發生),人們可以把它的點按從小到大的順序排列為。-S 0毛51CS:C...,並用隨機變數序列{Sn,nCO}或由Tn =S}-S。一,定義的點間間距序列{T
,n)l}表示該點過程.另一方面,若以N(t)記過程在區間(O,t]中發生的點數,則{N(t),t}0}是一計數過程;若給定了一計數過程{N(t),t妻0},則通過
可確定一點列{Sn,n)O}(如前,令So=0).由於這種一一對應關係,人們在數學上往往把一個點過程和相應的計數過程看做是等同物(參見“隨機測度”和“計數過程”).