隨機過程有限維分布族

隨機過程有限維分布族是(family of finite-di-mentional distributions of a stochastic process)由隨機過程在任意有限多個時刻的取值確定的有限維分布函式族。

定義

隨機過程有限維分布族(family of finite-di-mentional distributions of a stochastic process)由隨機過程在任意有限多個時刻的取值確定的有限維分布函式族.設{X(t),t∈T}是定義在機率空間上的實值隨機過程.對任意正整數n及任意，隨機變數X(t,),X(t2), "..}X (tn)的聯合分布函式就是Fil,iZ, },rn (x1 ,xz , ".. ,x,})=P (X (t,)鎮x,，X (t2)錢xz，…, X (tn)毛xn).當n在正整數集中變動，t,,tZ,...,t，在7,中變動時，所得到的分布函式族F = { Ft1 ,,Z,. .,}} (x, , x2 , ... } xn )”一1}2}...}tl,tZ}"..}tnET}稱為隨機過程{X (t),tET }的有限維分布函式族或有窮維分布族.有限維分布族具有如下兩個特徵性質:

特徵性質

相容證明

柯爾莫哥洛夫定理：設分布函式族{F(t1,t2,,tn；x1,x2,,xn),n ≥1}滿足對稱性和相容性,則必存在一個隨機過程{X(t),t∈T},其有限維分布恰好為此有限維分 布函式族．

相容性：設m

一致性

即時間可追溯性，對隨機過程的測量具有時間可追溯性，測量時間改變順序，不會改變測量結果，也就是說已發生的事即成為無法改變的歷史，縱使時光倒流。

用法

1.對(},2,"..,n)的任一排列(j，，j:，…，j。)及任意實數xl}x.z}...}x.n，有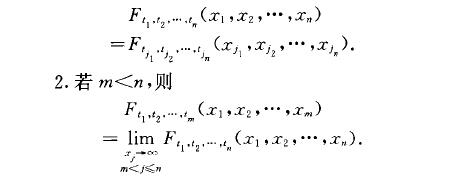

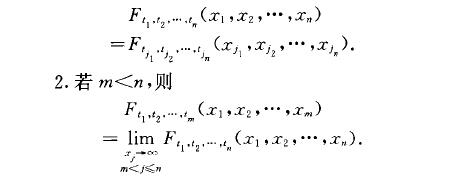
這兩個性質通常稱為相容性條件或一致性條件