隨機遊動模型

若時間序列{x_t}適合於模型x_t+x_t-1=ε_t，其中{ε_t}是均值為零，方差為σ_ε²的白噪聲序列，則稱其為隨機遊動模型。隨機遊動是一階自回歸模型[AR (1)]參數為a=1的極端情形。這時 {x_t}不具有平穩性， 因為上述模型可以化為： x_t=ε₁+...+ε_s+_...+ε_t，s=1,2,...,t，Var(x_t)隨t而增大，當t→∞時Var(x_t)→∞，時間序列分析一般不對隨機遊動模型進行探討研究。

基本介紹

• 中文名：隨機遊動模型
• 外文名：random walk model
• 所屬學科：數學
• 所屬問題：統計學（時間序列）
• 簡介：一階自回歸模型的參數a=1的情形
• 提出者：統計學家莫里斯·肯德爾

基本介紹

對於AR(1)模型

它的平穩性條件是。若，則不滿足平穩性條件。(1)就成為

稱為隨機遊動模型。表示遊動者在t時刻的位置，表示向前或向後的步幅。由(2)得到

顯然，是隨機過程，它是隨機衝擊在時間上的積累，其圖形如圖1所示。這說明歷史上的任何一次衝擊同目前的衝擊起著同樣的作用，而且不隨時向的推移而消失。這裡是初始值。因此，這些衝擊隨時間的推移累積起來，其圖像如圖1那樣隨機地漂移，因而這一過程是非平穩的。其自相關函式為

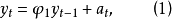
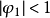
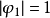
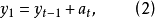
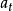
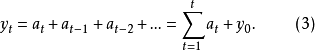
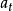
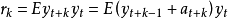
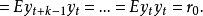
圖1

所以 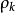=1，k=0，1，2，…

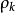
自相關函式的圖像如圖2所示。

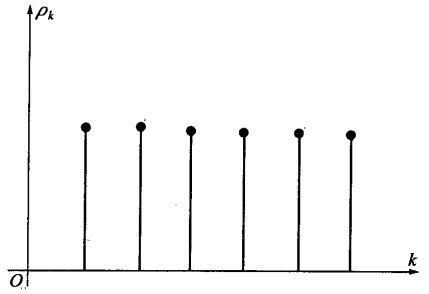圖2

的方差為

由此可見的方差隨t的增加而不斷增大，因此，是一非平穩序列。

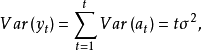
隨機遊動模型的經濟原型，是由統計學家莫里斯·肯德爾(Maurice Kendall)在1953年發現的。其背景是英國皇家統計學會1953年在倫敦開會，討論肯德爾寫的一篇有爭論的論文《經濟時間序列分析》的第一部分：《價格》。肯德爾的初衷是想藉助剛問世不久的電子計算機尋找股票價格波動的規律，但研究結果卻有意外的發現，股市價格不但沒有任何規律，而且就像一個醉漢走步一樣，下周的價格等於本周的價格加上一個隨機數字，也就是說股價近似遵從隨機遊動(RandomWalk)模型。

隨機遊動模型的種類

若(1)是下列形式

式中為非零常數，仍是隨機衝擊值，也就是白噪聲序列，則稱(4)為帶漂移項的隨機遊動模型。通過對(4)的直接疊代，可得

這裡是的初始值。由此可見的期望值為

方差為

方差隨t的不斷增加而不斷增大，因此是不平穩的隨機序列。

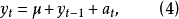
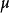
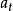
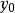
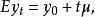
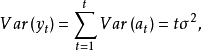
若(5)是如下形式

均為常數，則稱(6)為帶線性趨勢項的隨機遊動模型。