陳氏混沌系統

1999年，美國休斯頓大學陳關榮教授發現了一個新的混沌吸引子——Chen系統，即陳氏混沌系統，它與Lorenz系統類似，但不拓撲等價而且更複雜。混沌是非線性動力系統的固有特性，是非線性系統普遍存在的現象。

基本介紹

• 中文名：陳氏混沌系統
• 外文名：Chen Chaotic System                    
• 學科：控制科學與工程
• 提出者：陳關榮
• 時間：1999年
• 特點：不確定性、不可重複、不可預測

基本概念

1999年，美國休斯頓大學陳關榮教授發現了一個新的混沌吸引子——Chen系統，即陳氏混沌系統，它與Lorenz系統類似，但不拓撲等價而且更複雜。混沌系統是指在一個確定性系統中，存在著貌似隨機的不規則運動，其行為表現為不確定性、不可重複、不可預測，這就是混沌現象。混沌是非線性動力系統的固有特性，是非線性系統普遍存在的現象。

系統描述

1999年，陳關榮等人發現了一個與Lorenz混沌系統相類似但拓撲不等價的混沌吸引子，該系統描述如下（受控系統（1））：

陳氏混沌系統（Chen）為典型的混沌系統，當a=35，b=3，c=28時，系統呈現混沌狀態。陳氏混沌吸引子如圖所示：

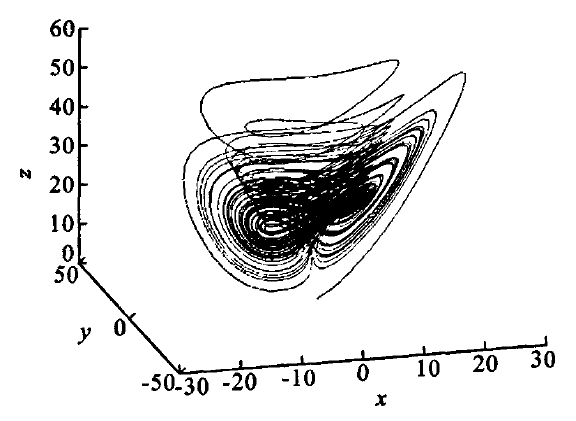
將各狀態變數看作相位連續、包絡隨機變化的諧和信號，系統的特徵頻率定義為信號相位的平均變化率，即

其中N為時間T內信號的波峰或波谷數目。對於陳氏系統可計算其特徵頻率為 ，由於參數c的變化對系統行為具有較大影響，可設計參數激勵非反饋控制系統如下：

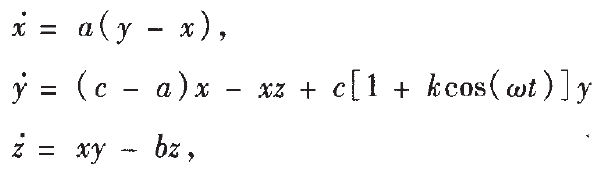
其中k是唯一的待定控制參數，激勵信號頻率 遠大於系統特徵頻率 ，通過調節參數k使陳氏混沌系統穩定於周期狀態或平衡點。

反饋控制方法分析

線性反饋控制陳氏混沌系統到平衡點

當a=35，b=3，c=28時，系統呈現混沌狀態。此時數學模型為

此時系統處於混沌狀態，有三個平衡點 ， ， 。 是鞍點， 和 是不穩定焦點，對系統進行數值仿真出現混沌圖形，軌線圍繞兩個不穩定焦點 和 隨機跳動，呈雙螺旋狀，如下圖所示：

構造線性反饋控制器，控制陳氏混沌系統到達平衡點S=(x,y,z)，作坐標平移變換，令

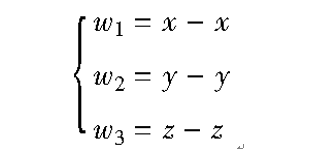
則受控系統（2）為：

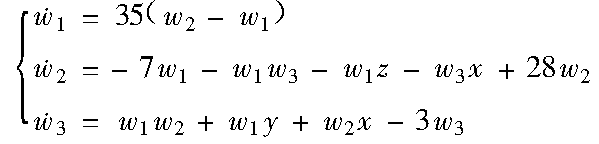
將線性反饋控制器 加到上述系統的第二個方程上，則受控系統（3）為

此時狀態W指數穩定於點W0(0，0，0)，亦即原系統可按指數全局穩定於平衡點S=(x,y,z)。

非線性反饋控制陳氏混沌系統到平衡點

對系統（2）的第二、第三個方程分別使用控制擾動：

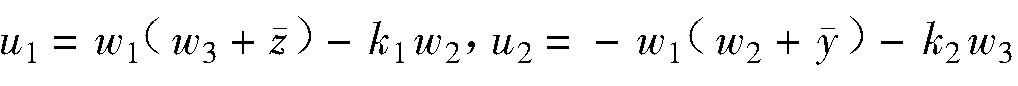
則受控系統（4）為：

顯然受控系統（4）與系統（2）有相同的不動點W0(0，0，0)，據Lyapunove穩定性原理，系統（2）能被控制到其平衡點，即原系統（1）能被控制到它的三個平衡點。

自適應控制

假定回響系統具有3個未知不確定參數，同樣假定系統式（1）為驅動系統，可以構建相應地回響系統（6）如下：

式中，u1，u2，u3為要設計的控制器。

由（6）減去（1）可得：

自適應控制目標是尋找合適的控制器 以及參數自適應律，使得系統式（6）能全局漸近同步於系統式（1），即 。

Lorenz系統和陳氏混沌系統

1963年，Lorenz發現了第一個混沌吸引子——Lorenz系統，從此揭開了混沌研究的序幕。人們不斷發現新的混沌奇異性，不斷地加深與統一對混沌的理解。1999年，美國休斯頓大學陳關榮教授發現了一個新的混沌吸引子——Chen系統，即陳氏混沌系統，它與Lorenz系統類似，但不拓撲等價而且更複雜。

Lorenz系統和陳氏混沌系統分別屬於兩個相反的類：

Lorenz系統滿足 ，而陳氏混沌系統卻滿足 ，在這種意義下，他們是對偶的兩個動力系統。由於陳氏混沌系統比Lorenz系統具有更複雜的拓撲結構和動力學行為，這一方面使得它在信息加密和保密通信等領域有著更廣闊的套用前景，另一方面使得陳氏混沌系統很難控制，許多對Lorenz系統輕而易舉的控制方法對陳氏混沌系統卻不太理想甚至無效。儘管如此，對該系統的控制已有不少有效的控制方法，如：逆最優控制、識別控制、數字控制、模糊控制、脈衝控制、自適應控制等，隨著研究的不斷深入，在實際套用中必然要追求實施控制的有效性、代價大小和難易程度。