限位排列關聯矩陣

限位排列的關聯矩陣(incidence matrix of forbidden permutation)是一個表征限位排列的(0，1)矩陣，通過對限位排列的關聯矩陣積和式的計算，可求出限位排列數，限位排列問題的研究可化為其相應的關聯矩陣的研究。

基本介紹

• 中文名：限位排列關聯矩陣
• 外文名：incidence matrix of forbidden permutation
• 所屬學科：數學
• 所屬問題：組合學（組合設計）
• 簡介：一個表征限位排列的(0，1)矩陣

基本介紹

若矩陣A=(a_ij)滿足條件：

則它稱為集合{1，2，…，n}對其子集族{A₁，A₂，…，A_m}的關聯矩陣，也稱為(A₁，A₂，…，A_m)限位排列的關聯矩陣。

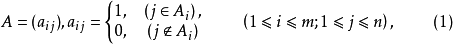
若A是(A₁，A₂，…，A_m)限位排列的關聯矩陣，則(0，x)矩陣xA稱為此(A₁，A₂，…，A_m)限位排列的(0，x)關聯矩陣，這裡xA=Ax=(a_ijx)，而

又稱A′=(a′_ij)為此(A₁，A₂，…，A_m)限位排列的(t，1)關聯矩陣，這裡

限位排列問題的研究可化為其相應的關聯矩陣的研究。

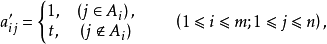
舉例

例如，n階更列問題的關聯矩陣是

n階既化ménage問題的關聯矩陣是

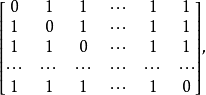
關聯矩陣的補

m×n的(0，1)矩陣A=(a_ij)的補矩陣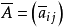是指滿足條件

的m×n的(0，1)矩陣，矩陣也稱為(A₁，A₂，…，A_m)限位排列的關聯矩陣A的補，與相應的限位排列問題，稱為原限位排列問題的補問題。一個限位排列問題的補問題與一個車問題相對應。

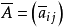
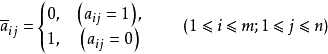
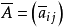
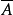
關聯矩陣(1)的補是

對待矩陣(2)可有兩種觀點。第一，可把(2)看作某一個限位排列問題——稱為原限位排列問題的補問題——的關聯矩陣，其限制條件正好是原限制條件的補：

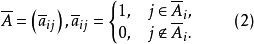
元j的限位集為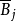，禁位集為B_j；

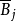
第i位的限元集為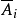，禁元集為A_i.

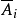
第二，可以把(2)看作一個棋陣，它由一個m×n的矩形棋盤上的mn個格子組成，每個格子要么是1，要么是零；把有1的格子稱為實格，其他格子稱為虛格。

如果約定，在棋陣的實格處不允許放上棋子，那么，()-限位排列問題就化為，尋求在棋陣(2)上放置m個互不相遇的棋子的放法的個數。這裡，所謂二個棋子相遇，意指它們在棋盤上的同一行或同一列。

形如(1)的矩陣共2^mn個，這是因為mn個a_ij之任一都可獨立地取零和1。自然，這裡把全1陣和零陣也計入在內，全1陣即無限制條件的m-無重排列的關聯矩陣。易知，對關聯矩陣的下面二種變化，並不影響限位排列問題的本質，最多只是對原來的限位排列問題換一種說法而已。

(1)關聯矩陣的轉置。此時只需把位和元的地位交換便得原限位排列問題；

(2)關聯矩陣的諸行互易位置，諸列互易位置。此時僅只把位和元都分別重新編號而已。

例如，只有一個元為1，其餘元皆為零的m×n矩陣共mn個，而這mn個矩陣可視為同一個限位排列問題的關聯矩陣，因為經變換(2)，可把這個1從一個位置變到其他任一指定的位置。