阿希士爾-列維坦積分逼近（approximation by Achieser-Levitan integrations）是逼近全實軸上連續函式的一種工具。
基本介紹
- 中文名：阿希士爾-列維坦積分逼近
- 外文名：approximation by Achieser-Levitan integrations
- 適用範圍：數理科學
簡介,性質,連續函式,
簡介
阿希士爾-列維坦積分逼近是逼近全實軸上連續函式的一種工具。
設f(x)是(-∞,+∞)上的有界且連續的函式，r≥0，σ>0，則稱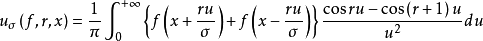
為f的阿希士爾-列維坦積分。
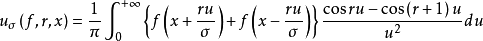
性質
阿希士爾-列維坦積分是指數≤(r+1)σ/r的指數型整函式，而且若f(x)是在(-∞,+∞)上有界的且指數≤σ的整函式，則uσ(f,r,x)≡f(x)。
若f(x)在(-∞,+∞)上有界連續，則用uσ(f,r,x)對f(x)的逼近稱為阿希士爾-列維坦積分的逼近；此時還有
其中Cr>0僅與r有關，Aα(f)是σ階整函式對f的最佳逼近值。
連續函式
函式y=f(x)當自變數x的變化很小時，所引起的因變數y的變化也很小。例如，氣溫隨時間變化，只要時間變化很小，氣溫的變化也是很小的；又如，自由落體的位移隨時間變化，只要時間變化足夠短，位移的變化也是很小的。
